с математикой! Решить без использования теории суммы рядов и т.п., используя знания на уровне 7-8 класса
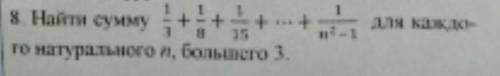
Другие вопросы по теме Математика
Популярные вопросы
- Як відредагувати вислів: ця дівчина одразу кинулася мені в очі...
1 - Сточное или нет озеро эйр норд? если да, то какие реки...
2 - Сколько спирта нужно сжечь чтобы 200 г воды при температуре 20 градусов...
3 - 20б. написать краткое содержание (либретто) рок-оперы юнона и авось...
2 - Знайдіть чотири послідовних цілих числа,якщо добуток першого і третього...
3 - Сравни поставь знак: 8 м 5 дм 4 см - 763 м - 6 м 87 см...
2 - Напишите рассказ на тему человек и человек по обществознанею 6 класс...
1 - Скниги «зеленые страницы» примеры других видов животных. запишите...
3 - Определить массу меди полученную восстановлению её оксида m=320...
2 - Написать сочинение на тему: кто ты по национальности и твой традиций(я...
1
1/(n^2 - 1) = (n + 1 - (n - 1))/2((n - 1)(n + 1)) = 1/2(1/(n-1) - 1/(n+1))
1/3 = 1/2(1 - 1/3)
1/8 = 1/2 (1/2 - 1/4)
1/15 = 1/2(1/3 - 1/5)
1/3 + 1/8 + + 1/(n^2 - 1) = 1/2(1 - 1/3 + 1/2 - 1/4 + 1/3 - 1/5 + 1/4 - 1/6 +...+ 1/(n-2) - 1/n + 1/(n - 1) - 1/(n + 1)) =1/2(1 + 1/2 - 1/n - 1/(n + 1)) = (3n^2 +n -1)/4n(n+1)
1/n + 1/(n+1) = (2n+1)/n(n+1)
3/2 - (2n+1)/n(n+1) = (3n^2 + 3n - 2n - 1)/2n(n+1)
ответ (3n^2 +n -1)/4n(n+1)
1/(n²-1)=1/(2*(n-1))-1/(2*(n+1))=0.5*((1/(n-1))-(1/(n+1)))
n=2; а₂=0.5*(1-1/3)=1/3
n=3; а₃=0.5*(1/2-1/4)=1/8
n=4; a₄=0.5*(1/3-1/5)=0.5*2/15=1/15
n=5; а₅=0.5*(1/4-1/6)=1/24
n=6; а₆=0.5*(1/5-1/7)=1/35
n=7 ; а₇=0.5*(1/6-1/8)=1/48
s=1/3+1/8+1/15+..+1/(n²-1)=0.5*(1-1/3+1/2-1/4+1/3-1/5+1/4-1/6+1/5-1/7+1/6-1/8+...+
1/(n-1))-(1/(n+1)));
очевидно, если устремить n⇒∞, то последняя дробь обратится в нуль. Тогда сумма ряда равна 0.5*(1+1/2)=3/4, но условием предусмотрено найти сумму раяда для n>3, т.е. от 3/4 надо отнять сумму двух первых членов (1/3+1/8)=11/24
3/4-11/24=(18-11)/24=7/24