с математикой. 1 - дифференциальные уравнения, 2 - задача коши
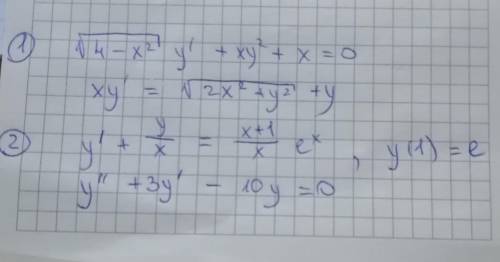
Другие вопросы по теме Математика
Популярные вопросы
- Даю 30б. Как на французском языке будет : Привет, Милиса, как дела?...
3 - Найдите слово, в котором нужно вставить И. Подпись отсутствует 1) без...дейный...
3 - 18.Счет на табло 40 - 15. Игрок 1 подает на матч, выполняет подачу без...
1 - Проведите синтаксический разбор Тополь, по воле человека посаженный для...
1 - В ячейку ввели следующие символы:=СУММ(C8:C12;H5:H8)Данные какого типа...
2 - 1. Подростки радуются, когда ... 2. Подростки огорчаются, когда ... 3....
1 - выписать ход основных событий Гражданской войны на территории Горного...
2 - Два точечных заряда q1 = 10 нКл и q2 = 30 нКл находятся на расстоянии...
3 - Записать цифрами, какие прыжки к каким видам относятся Опорные прыжки:...
2 - Нужно сделать цитатный план стихотворений Ф.Тютчева Неохотно и несмело...
1
1.
общее решение
2.
общее решение
3.
решаем по частям:
получаем:
общее решение
частное
4.
общее решение