С интегральной формулы Коши или формулы типа Коши вычислить:

Пошаговое объяснение:

Подынтегральная функция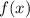 имеет два простых нуля в области, ограниченной контуром :

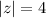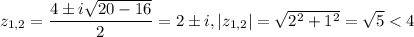
А потому введем внутренние непересекающиеся контуры, например -

и . Тогда в области , ограниченной окружностью и указанными внутренними контурами, подынтегральная функция аналитическая, а внутри каждой из областей, ограниченных внутренними контурами, имеет ровно один ноль, и он простой.

А тогда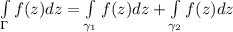

Значит

Подставляя вычисленные значения, получим