1. Математика
  2. с геометрией хотя бы один

с геометрией хотя бы один номер...​


с геометрией хотя бы один номер...​

mokantatiana mokantatiana    1   21.01.2021 18:39    0

Ответы
andreu1024 andreu1024  21.01.2021 18:40

Формулы, которыми мы будем пользоваться:

Длина окружности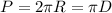 P = 2\pi R=\pi D

Площадь окружности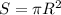 S = \pi R^2

Пошаговое объяснение:

1.1 Утверждение неверное, так как отношение длины окружности к диаметру всегда равно Пи для всех окружностей (см. формулу длины окружности)

1.2 Да, утверждение верное, так как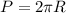 P = 2\pi R, и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза

1.3 Данное утверждение неверно, т.к. зависимость площади круга от радиуса не линейна, а квадратична. То есть, если мы уменьшим радиус в два раза, то площадь уменьшится в 4 раза.

1.4 Верно, см. объяснение в 1.3

2. Воспользуемся формулой вычисления длины круга, приведённой вначале:

P=2\pi R\\23\pi =2\pi R\\R=\frac{23\pi }{2\pi} =11.5

3. Воспользуемся формулой вычисления площади круга, приведённой вначале:

S=\pi R^{2} \\49\pi =\pi R^2\\R=\sqrt{\frac{49\pi}{\pi}} =7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Dmitry321123 Dmitry321123  26.04.2021 11:21
11.Биссектриса разделила угол АВС на два угла, каждый из которых содержит 68°. Какова величина угла ABC ?А) 34°. Б)86°. В) 126°. Г) 136°.No12. Определите вид угла, если...
пллсыео пллсыео  26.04.2021 11:21
Акелинди 8 алма калды -? 3 есе артык​...
человек9527 человек9527  26.04.2021 11:20
БАРИА 2 1.В ряду чисел 3,8; 15; 30, 24 пропущено одню ЧИСЛО. Найдите его, еслиа) мода ряда равна 15 ( )б) размах ряда равен 50 ( )в) среднее арифметическое ряда равно 18...
sashaorlov2006 sashaorlov2006  26.04.2021 11:20
мастер вы январе приготовил 300 деталей но феврале 405 на сколько процентов выросло продуктивность мастера если известно что длительность работы была одинакова...
новинький2 новинький2  26.04.2021 11:20
На шахматном турнире учеников 6го класса получили 13.13.12.13.10.13.12.10очков найдите: а)средне арифметическое Б)размах В)молу...
dashhach dashhach  26.04.2021 11:19
6) (x - 5)(x + 3) = 0; B Записать корни...
kkdyming48kg kkdyming48kg  26.04.2021 11:19
надо решить, кто какой сможет...
vovalomov00 vovalomov00  26.04.2021 11:19
В школе 1500 учеников. Из них 42% составляют мальчики. Сколько мальчиков в школе? ​...
krepkinapolina29 krepkinapolina29  26.04.2021 11:19
В пирамиде АВСМ ребро МС перпендикулярно плоскости АВС. В треугольнике АМВ (АМ=14 см, ВМ=12см, АВ=10см) провели среднюю линию KL. Вычислите радиус окружности, которую можно...
kakniet kakniet  26.04.2021 11:19
Найти значение зависимой переменной у = - 0,2 х + 3 при х = 5?...

Популярные вопросы