С дифференциала функции вычислить приближенно
под корнем 49,49
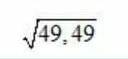
Другие вопросы по теме Математика
Популярные вопросы
- Контрольная работа 13 5 КЛАСС Углы. Измерение углов. Круговые диаграммы...
1 - 2. Используя данные таблицы 5 из темы 54, определите, во сколько раз быстрее...
3 - Задача: Проанализировав ситуацию, участникам необходимо определить должен...
3 - ть виконати завдання) біологія...
1 - Дати фізико-географічну характеристику зони Полісся використовуючи власний...
1 - Найди в словах автора (комментирующей части) глаголы речи и запиши их...
1 - Добрый вечер с англ.языком. Упражнение 3 Образуйте сравнительную и превосходную...
3 - Саша Черный Кавказкий пленник дайте характеристику героям и их поступкам....
1 - Реагируют ли оксид марганца ( MnO2) и сероводород?...
2 - Назвать причины, по которым Александр Невский сражался со шведами и тевтонцами,...
2
ответ: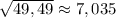
Пошаговое объяснение:
Необходимо найти приближенное значение функции √х при значении аргумента x₀ = 49 и приращении аргумента Δx = 0,49
Для приближенного вычисления значения функции применяется следующая формула:
f(x₀+Δx) ≈ f(x₀) + f'(x₀)·Δx
В нашем случае
f(49+0,49) ≈ f(49) + f'(49)·0,49
По заданию задана функция √х
Найдем значение функции
f(49) = √49 = 7
Найдем значение производной
При х₀ = 49
Находим приближенное значение функции в точке 49,49