с 1м и 2м интегралом (35б)
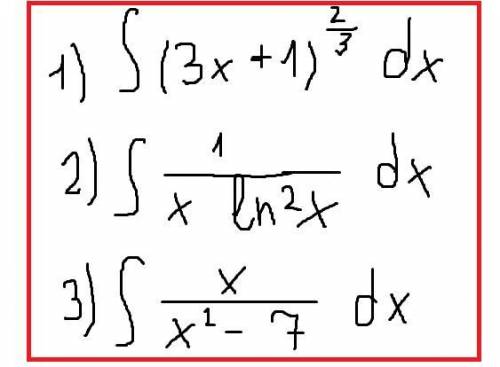
Другие вопросы по теме Математика
Популярные вопросы
- Какой частью речи является слово еще...
3 - Отгодайте одинаковые слова,загаданые тройками пословиц. он поёт...
2 - Добавить дар, дер, тар, тер, лар, лер, к словам қорық, барыс,...
1 - Девочке подарили для коллекции 6 копеек двумя монетами.какие это...
1 - Что происходит с тарасом бульбой после казни остапа...
3 - Образуйте однокоренное прилагательное к слову доблесть запиши...
1 - Нужно подготовить маленькое сообщение о малых небесных телах примерно...
3 - Системные программы – это средства, предназначенные для создания...
2 - Какая папка является вершиной графического интерфейса операционной...
1 - Боровик придумать вопрос для кроссворда...
2
Пошаговое объяснение:
1)
2)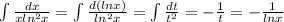
Пошаговое объяснение:
1)
\begin{gathered}\int\limits {(3x+1)^{\frac{2}{3} }} \, dx =\frac{1}{3}\int\limits {t}^{\frac{2}{3} } \, dt=\\=\frac{1}{3}*\frac{t^{\frac{2}{3} +1}}{\frac{2}{3} +1}= \frac{1}{3}* \frac{3}{5}t^{\frac{5}{3}}=\frac{1}{5}*(3x+1)^{\frac{5}{3}}\\3x+1=t; 3dx=dt; \\dx=\frac{1}{3}dt\end{gathered}
∫(3x+1)
3
2
dx=
3
1
∫t
3
2
dt=
=
3
1
∗
3
2
+1
t
3
2
+1
=
3
1
∗
5
3
t
3
5
=
5
1
∗(3x+1)
3
5
3x+1=t;3dx=dt;
dx=
3
1
dt
2)\int \frac{dx}{xln^2x}=\int \frac{d(lnx)}{ln^2x}=\int \frac{dt}{t^2}=-\frac{1}{t}=-\frac{1}{lnx}∫
xln
2
x
dx
=∫
ln
2
x
d(lnx)
=∫
t
2
dt
=−
t
1
=−
lnx
1