Розвяжіть рівняння |х+2|×(-х+1)=0

Розв'яжемо рівняння |x+2| × (-x+1) = 0 шляхом розгляду двох можливих випадків:

|x+2| = 0:

Якщо |x+2| дорівнює нулю, це означає, що x+2 = 0.

Розв'язок цього рівняння: x = -2.

-x+1 = 0:

Якщо -x+1 дорівнює нулю, це означає, що -x = -1.

Множимо обидві частини на -1, щоб змінити знак: x = 1.

Таким чином, рівняння має два розв'язки: x = -2 і x = 1.

Покрокове пояснення:

x = -2; x = 1

Пошаговое объяснение:

|х+2|*(-х+1)=0
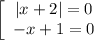
Произведение равняется нулю, когда хотя бы один из множителей равен нулю

Из теории известно, что |a| = b <=> a = ±b, при b>0