. Розв’язати задачу використовуючи основні поняття, теореми та формули теми «Дискретні випадкові величини»: для даних випадкових величин скласти закон розподілу, знайти математичне сподівання , дисперсію та середнє квадратичне відхилення . В ящику 5 білих, 3 чорних та 4 синіх кульки. Навмання виймають 2 кульки. Тут {число білих кульок серед вилучених}
Другие вопросы по теме Математика
Популярные вопросы
- Установите состав сплава (в массовых процентах), состоящего из алюминия,...
2 - Два одинаковых небольших шарика массой по 0,1 кг подвешены в одной точке...
2 - При взаємодії етанолу і оцтової кислоти масою 5,6 г добули естер. Визначити...
1 - Найдите значение выражения 162cos²(6a-3p/2), если cos3a=2/3...
1 - Превращение бутана в бутен относится к реакции ? 1.дегидратации2.изомеризации3.дегидрирования4.полимеризации...
2 - Стороны ромба образует его диагоналями углы из которых в 2 раза больше....
1 - Почему православие стало одним из главных факторов объединения русских...
2 - О Чём расказал мне оченний...
1 - Как решить пример? 875+p÷121=1999...
2 - 1)Напишите уравнение реакции восстановления меди алюминием. 2)Напишите...
1
Розглянемо випадкову величину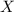 — число білих кульок серед вилучених.
— число білих кульок серед вилучених.
Всього можливих подій: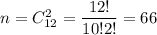 .
.
1) Імовірність того, що серед навмання вилучених 2 кульок не буде білої :
2) Імовірність того, що серед навмання вилучених 2 кульок буде одна біла кулька:
3) Імовірність того, що серед навмання вилучених 2 кульок всі кульки будуть білими:
Закон розподілу випадкової величини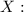
Xi 0 1 2
Pi 7/22 35/66 5/33
Знайдемо математичне сподівання випадкової величини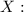
Дисперсія випадкової величини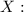
Середнє квадратичне відхилення: