1. Математика
  2. родненькие, с примерами

родненькие, с примерами из высшей:


родненькие, с примерами из высшей:

vikatormash09 vikatormash09    3   07.07.2020 15:52    4

Ответы
мугамбе мугамбе  15.10.2020 15:16

Пошаговое объяснение:

1.

\lim_{n \to \infty} \frac{n^3}{2^n}

исследуем по признаку Даламбера

\lim_{n \to \infty} \frac{u_{n+1}}{u_n } =q

если q < 1, то ряд расходится, если q > 1, то сходится, если =1 неопределенность

\lim_{n \to \infty} \frac{(n+1)^3}{2^{n+1}} : \frac{n^3}{2^n} = \lim_{n \to \infty} \frac{(n+1)^3}{2n^3} = \frac{1}{2}

ряд сходится

2.

область сходимости ряда это [-R; R], где

R= \lim_{n \to \infty} \frac{a_n }{a_{n+1}}

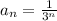
у нас      a_n = \frac{1}{3^n}

R= \lim_{n \to \infty} \frac{3*3^n }{3^n}} = 3

x₁ = 1-3 = -2

x₂ = 1+3 = 4

ряд абсолютно  сходится при всех x ∈ (-2;4)

теперь на концах

х  = -2

∑ 1/3ⁿ *(-3)ⁿ = (-1)ⁿ

знакочередующийся ряд

по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего.

у нас 1=1=1 - не выполняется.

по второму признаку - предел ряда должен стремиться к нулю (при n стремящейся к бесконечности)

у нас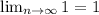 \lim_{n \to \infty} 1 = 1

точка х = -2 есть точка расходимости

х = 4

исследуем при интегрального признака сходимости

\int\limits^ \infty}_0 {1} \, dn = (n) I_0^ \infty = \infty

точка х = 4 так же точка расходимости

3.

тут я не совсем уверена. вот что помню из института....

erf(x) = \frac{2}{\sqrt{\pi } } \int\limits^x_0 {e^{-t^2}} \, dt

так что, извините, если что не так

\int\limits^{1/5}_0 {e^{(-5x^2)} \, dx

\int\limits^{1/5}_0 {e^{(-5x^2)} \, dx = \frac{\sqrt{5} \sqrt{\pi} *erf(\sqrt{5}*x)}{10} I_0^{\frac{1}{5}} = 0.187.....

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Angel168Demon Angel168Demon  12.09.2019 00:50
Коля, дима и саша собрали вместе 30 грибов. дима нашёл в два раза больше грибов чем коля. а коля в три раза меньше чем саша . сколько грибов нашёл каждый из них....
PomogitePLS111 PomogitePLS111  12.09.2019 00:50
Решить . масса сушеных яблок составляет 16% массы свежих яблок. сколько сушёных яблок получится из 2,5 т свежих яблок....
DenisKazansev DenisKazansev  12.09.2019 00:50
Такое. вы пишите и напишите а) правильною дробь б) непрвальнаб дроби : 12/13; 15/15; 15/17/15; 2/21; 9/20; 25/29; 41/40; 55/43...
TheJurasikBint TheJurasikBint  12.09.2019 00:50
Сапожник за 4 дня с jj 12 пар сапогов за какое время он же шьет 135 пар сапог...
Mika123123 Mika123123  12.09.2019 00:50
На сковороде помещается 2 куска хлеба на поджаривание куска с одной стороны требуется 1 минута как поджарить за 3 минуты три кусочка хлеба с обеих сторон? по рпс...
HollywooD2016 HollywooD2016  12.09.2019 00:50
Для приготовления теста берут 4 части муки и 2 части молока и одну часть сметаны. сколько молока надо взять чтобы приготовить 2 кг 100 г теста в такой пропорции?...
vanyad09 vanyad09  12.09.2019 00:50
Даны три числа, сумма которых ровна 333. первое число больше второго на 6, а третье число меньше второго на 6. найдите меньшее из этих трех чисел....
igor1337d igor1337d  12.09.2019 00:50
Знайдiть 4/7 вiд частки чисел 1 5/16 i 1 1/2 а) 2, б) 1/3, в)0,5 г) 4...
рябов2005 рябов2005  12.09.2019 00:50
Составьте 3 примера про безопасные, отсительно безопасняе, огнеопасные, и ядовитые веществах...
Ekaterina152005 Ekaterina152005  12.09.2019 00:50
125 человек на банкете 90 съели по куску пирога, 100 съели по куску торта. сколько человек не ели торт? сколько человек не ели пирог? сколько человек съели и пирог и торт...

Популярные вопросы