(Ресурсная задача)
Для изготовления изделий типа А и В используется сырье трех
видов, запасы каждого из которых Р1 , Р 2 , Р3 . На производство
одного изделия типа А требуется затратить а1 кг сырья первого вида, а2 кг сырья второго вида, а 3 кг сырья третьего вида. На одно
изделие типа В расходуется соответственно b1 , b 2 , b 3 кг сырья
каждого вида. Прибыль от реализации единицы изделия А составляет α /ден. ед., а изделия В – β /ден. ед. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их
реализации. Решить задачу симплекс-методом. Дать геометрическое истолкование задачи. Все данные приведены снизу
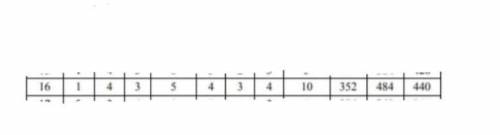
Другие вопросы по теме Математика
Популярные вопросы
- Определите момент инерции небольшого карандаша длиной 30 см и массой 50...
3 - Облечение нравственнвх пороков общества (по сказке М.Е. Салтыкова- Щедрина...
3 - Почему за просто какие-то ответы надо смотреть либо рекламу с рекламой либо...
1 - Перепишіть, вибираючи з дужок велику чи малу літеру. Свій вибір обґрунтуйте....
3 - Кос кала табиғаты такырыбына матн жаз...
3 - Написать пересказ Заячьи лапы...
1 - Система образов в произведении Пушкина Братья-разбойники...
3 - Продолжите данный текст Укажите разряд числительных ...
2 - C12h22o6 + Ag O3 составить уравнение реакции...
3 - Я не понимаю почему, но у меня на левой ноге волосы по левую сторону ноги...
2
Перед нами стоит задача составить план производства изделий А и В, чтобы получить максимальную прибыль от их реализации. У нас есть затраты сырья каждого вида на изготовление одного изделия каждого типа и запасы сырья каждого вида.
Для начала, давайте введем обозначения:
- Пусть х - количество изделий типа А, которые мы хотим произвести
- Пусть у - количество изделий типа В, которые мы хотим произвести
Теперь нам нужно составить систему уравнений, учитывая затраты сырья каждого вида на производство каждого изделия и имеющиеся запасы сырья:
1) а1х + b1у ≤ Р1
2) а2х + b2у ≤ Р2
3) а3х + b3у ≤ Р3
Также, нам нужно учесть, что мы хотим максимизировать прибыль. Выражение для прибыли от производства изделий будет: αх + βу
Таким образом, мы сформулировали следующую задачу линейного программирования:
Максимизировать:
αх + βу
При ограничениях:
а1х + b1у ≤ Р1,
а2х + b2у ≤ Р2,
а3х + b3у ≤ Р3,
х ≥ 0, у ≥ 0.
Теперь приступим к решению этой задачи симплекс-методом.
1. Для начала, приведем систему уравнений к канонической форме, добавив фиктивные переменные. Обозначим их z1, z2 и z3:
а1х + b1у + z1 = Р1,
а2х + b2у + z2 = Р2,
а3х + b3у + z3 = Р3.
2. Теперь составим симплекс-таблицу:
| Базис | С | z1 | z2 | z3 | b |
|________|______________|______|______|______|__________|
| x | а1 | 1 | 0 | 0 | Р1 |
| y | b1 | 0 | 1 | 0 | Р1 |
| z1 | 0 | -1 | 0 | 0 | -Р1 |
| z2 | 0 | 0 | 0 | 1 | -Р2 |
| z3 | 0 | 0 | -1 | 0 | -Р3 |
3. Выберем ведущим столбец. В этом примере, максимум возможен только для alpha*x и beta*y, поэтому ведущим столбцом будет столбец с переменными x и y. Вычислим отношения свободных членов к значениям ведущего столбца:
|Ведущий столбец | Отношение |
|________________|__________|
| а1 | Р1/а1 |
| b1 | Р2/b1 |
4. Выберем ведущую строку. В нашем случае, отношение Р2/b1 наименьшее, поэтому выберем строку с переменной y как ведущую строку.
5. Произведем пересчет элементов симплекс-таблицы, используя выбранные ведущую строку и столбец. Ведущий элемент - b1.
| Базис | С | z1 | z2 | z3 | b |
|________|______________|______|______|______|__________|
| x | а1 | 1 | 0 | 0 | Р1 |
| y | b1 | 0 | 1 | 0 | Р1 |
| z1 | 0 | -1 | 0 | 0 | -Р1 |
| z2 | 0 | 0 | 0 | 1 | -Р2 |
| z3 | 0 | 0 | -1 | 0 | -Р3 |
6. Продолжим итерацию симплекс-метода до тех пор, пока не будет достигнуто оптимальное решение.
Геометрическое истолкование задачи заключается в поиске оптимальной точки в пространстве ограничений. Задача сводится к поиску такой точки, которая максимизирует прибыль и удовлетворяет ограничениям на запасы сырья.
Надеюсь, данное объяснение помогло вам понять решение задачи. Если у вас остались какие-либо вопросы или требуется дополнительное объяснение, пожалуйста, дайте мне знать!