1. Математика
  2. решыте ! всьо заданое на

решыте ! всьо заданое на фото


решыте ! всьо заданое на фото

annvs1 annvs1    3   11.01.2021 15:06    0

Ответы
lizabjnyjyve lizabjnyjyve  10.02.2021 15:07

Пошаговое объяснение:

1. на фото

там сумма ряда рападается на суммы двух бесконечно убываюших геометрических прогресси. суммы этих прогрессий рассчитываются по формуле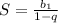     S = \frac{b_1}{1-q}

в конечном итоге общая сумма ряда = 1/6. ряд сходится

2. здесь будем рассматривать предел ряда по второму замечательному пределу

\lim_{n \to \infty} (1+\frac{a}{n} )^{bn} = e^{ab}

\lim_{n \to \infty} \frac{(2n-1)^n}{2n^n}= \lim_{n \to \infty} (1+\frac{-1}{2n} )^{\frac{1}{2} *2n}=e^{-1*(1/2)}= \frac{1}{\sqrt{e} }

таким образом предел не равен 0. необходимое условие сходимости не выполняется, следовательно, ряд расходится.


решыте ! всьо заданое на фото
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Lola1986 Lola1986  15.09.2019 12:00
Преобразуйте выражение в тождественно равное,используя переместительное и сочетательное свойства умножения. подчеркните коэффициенты -3/4x ×(-2/3y)×(1/2z)...
ovosh228322 ovosh228322  15.09.2019 12:00
По окончании футбольного турнира были названы 11 лучших футболистов среди них из команды факел было 5 футболистов из команды ракета два футболиста остальные из команды...
саят17 саят17  15.09.2019 12:00
Длина площадки прямоугольной формы равна 60 метров,а ширина- 10 метров.найди её площадь...
Саша12811 Саша12811  15.09.2019 12:00
Бассейн объемом 60 м3 наполняется через первую трубу за 3 ч, через вторую за 2 ч. за какое время наполнится бассейн через две трубы...
foxylol1 foxylol1  15.09.2019 12:00
Найди значиние выражений. 8м 52см х 28 = 224т 8ц х 62 = 9лет 6мес. + 13лет 8мес. = найди значение выражения. ( 119.628 - 1.356 х 18 : 6 + 87.588 ) : 9 =...
sirghiina sirghiina  15.09.2019 12:00
1) 3b(a-b); 2) 7m(m-n-p); 3) 5/12(-4x-6y-3)....
13022010 13022010  15.09.2019 12:00
Сплав состоит из меди и цинка в первом куске 60% меди и цинка 40% а во втором это соотношение равно 7: 3. сколько следует взять от каждого куска, чтобы получилось 1 кг...
Infasotka41 Infasotka41  15.09.2019 12:00
Факты о исследовании мирового океана мне нужно много !...
lermolen lermolen  15.09.2019 12:00
Основания равнобедренной трапеции равны 10 и 28 боковая сторона 15 . найдите площадь трапеции...
Sashapro111 Sashapro111  15.09.2019 12:00
Условия и решения найдите 1) 24л фруктого сока разлили в 8банок поровну.сколько надо таких банок,чтобы разлить 18л сока ? 21л сока? и 91стр автор моро...

Популярные вопросы