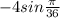Решите задачу с параметром
Желательно с объяснением

Другие вопросы по теме Математика
Популярные вопросы
- Найдите первый член арифметической прогрессии,если а_18=-9.6,d=0.8...
1 - Рассчитать массовую долю в азотистой кислоте...
1 - Произвести морфологический разбор глагола пение...
2 - Тепловой двигатель совершает за цикл работу 100 дж, какое количество...
1 - Проходит ли диагонали ромба через центр окружности ?...
3 - Под огороды жителям посёлка было отведено 15га 46а земли.хозяйственные...
3 - Спутник пролетает 84000км за 3ч. за какое время он пролетит 420000км,если...
3 - Подумайте,каковы главеые причины поражения в войне с римлянами...
3 - Дробь и найти числовое значение. а^(2)-8a+16 дробная черта ах-4х...
1 - Систематическое положение лепидосирена южноамериканского...
3
Далее, раставляя точки на прямой и находя соответствующие значения функции, определяем минимум и максимум.
Максимальное значение в точке x =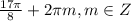 , минимальное -
, минимальное - 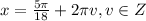
Найдем этим значения:
ответ: