1. Математика
  2. Решите задачу : Найти площадь

Решите задачу : Найти площадь криволинейной трапеции y= x^2+3 , если расписать подробно с рисунком

antiangel18 antiangel18    2   16.06.2021 11:09    1

Ответы
Дора18119 Дора18119  16.07.2021 11:12

Вспомним формулу Ньютона-Лейбница, которая посчитать площадь под графиком функции от a до b:

                              \displaystyle \int\limits^{b}_{a} {f(x)} \, dx = F(x) \;\; \Big|^{b}_{a} = F(b)-F(a)

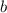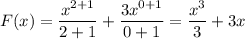Первообразная от f(x)=x^2+3  -  это F(x)=\dfrac{x^{2+1}}{2+1}+\dfrac{3x^{0+1}}{0+1}=\dfrac{x^3}{3}+3x.

            \displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \int\limits^{2}_{-1} {\Big(x^2+3\Big)} \, dx = \frac{x^3}{3} + 3x \;\; \Big|^{2}_{-1} = \\\\ = \bigg(\frac{2^3}{3}+3\cdot2 \bigg) - \bigg(\frac{(-1)^3}{3}+3\cdot(-1) \bigg) = \frac{8}{3} + 6 + \frac{1}{3}+3 = 12

Значит, искомая площадь равна 12. Задача решена!

ответ: 12
Решите задачу : Найти площадь криволинейной трапеции y= x^2+3 , если расписать подробно с рисунком
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kskvortsovak07 kskvortsovak07  11.08.2019 23:00
Решить: 125-(49+(у-1))=23 ; 124+(56-r)+36=172 ; 285+(х/14/481)=366 ; 224+(105+(32-х))=330 ; 450/(25+5*х)15...
Iriska91l23 Iriska91l23  11.08.2019 23:00
Как сделать вот эту посмотреть сумма уменьшаемого вычитаемого и разности равна 100 а потом найди уменьшаемое как сделать эту 3адачу...
TOLIK474747 TOLIK474747  11.08.2019 23:00
1площадь параллелограмма abcd равна 176. точка e — середина стороны ad. найдите площадь трапеции aecb. 2)в прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив...
elenavalkova92 elenavalkova92  11.08.2019 23:00
Составьте выражение: сумма чатного 105009 и 493 и частного 11803: 29. вычислите значение этого выражения...
Katpo Katpo  11.08.2019 23:00
Средства передвижения древнего человека....
arhivnaykr arhivnaykr  11.08.2019 22:50
Вы мимо дома номер которого равен 2p плюс один нечетная сторона улицы нескольких домов по этой стороне улицы еще нужно пройти чтобы дойти до дома номер которого в 5 раз больше...
sw321 sw321  11.08.2019 22:50
60 миллиардов 17 миллионов 3 ед-какая цифра стоит в разряде сотен миллионов этого числа? ....
МАРИЯpahal МАРИЯpahal  11.08.2019 22:50
Mасса мешка с мукой на25 кг больше массы половины этого мешка. чему равна масса всего мешка?...
Alexandr201755 Alexandr201755  11.08.2019 22:50
Решите систему неравенств система из: 2х+7больше 0 3х+4меньше 0...
kolesnikov20021 kolesnikov20021  11.08.2019 22:50
Собрались в поход.они решили,что возьмут только необходимое количество воды: 2л на каждые 10 км.руководитель группы проложил по карте маршрут,отметил расстояние 11 см и конечную...

Популярные вопросы