Решите уравнения: а) φ ( x )= 2 б) φ ( x )= 8 в) φ ( x )= 12 г) φ ( x )= 14

φ ( x ) - это функция, которая равна количеству натуральных чисел, меньших x и взаимно простых с x

Ответы

odinokijcelovek 06.10.2020 00:26

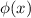Вообще $\phi(x)$ - функция Эйлера.

Нам нужно число справа представить как произведение простых чисел (каждое в какой-то степени), есть формула, по которой вычисляется эта функция в таком случае:

$\phi(x)=(p_1^{\alpha_1}-p_1^{\alpha-1})(p_2^{\beta}-p_2^{\beta-1})\cdot...\cdot(p_k^{\lambda}-p_k^{\lambda-1});\\ x=p_1^{\alpha}\cdot p_2^{\beta}\cdot ...\cdot p_k^{\lambda}$

Вообще такие уравнения просто по формулам не решаются. Но можно составить что-то вроде рекомендаций:

Проверить число, следующее за числом в правой части. Если оно простое, то оно пойдет в ответ.

Далее, функция Эйлера является мультипликативной, то есть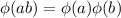 $\phi(ab)=\phi(a)\phi(b)$ , если a и b - взаимно простые числа.

Тогда имеем формулу: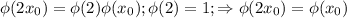 $\phi(2x_0)=\phi(2)\phi(x_0); \phi(2)=1; \Rightarrow \phi(2x_0)=\phi(x_0)$ , если 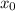x_0 - простое число.

Вообще с числом "2" много проблем возникает.

Далее, функция Эйлера - четное число, поэтому надо подобрать четные делители функции, которые представляются в виде р - 1.

Теперь попытаемся на примерах:

а) Здесь проще все корни подбором найти. Но вот применим "рекомендацию" про простое число. 2+1=3. 3 - простое число, значит x=3. И (3;2)=1 (кстати, НОД всегда ищется от n+1 (n - правая часть, я имею в виду) и двойки. Тогда x=3*2=6. Есть ещё один корень x=4 (просто подбором ищется). Больше корней нет.

ответ: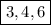 $\boxed{3,4,6}$

б) Вот здесь будем по-нормальному пытаться решать:

8=(3-1)(5-1)

Тогда корень равен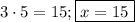 $3\cdot5=15; \boxed{x=15}$

$(15;2)=1 \Rightarrow x=2\cdot15=30; \boxed{x=30}$

Далее,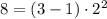 $8=(3-1)\cdot2^2$

Вот здесь корень ищется с домножением на 2 (т.е. если в разложении правой части присутствует двойка):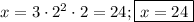 $x=3\cdot2^2\cdot2=24; \boxed{x=24}$

Кстати, отсылка к пункту а). 2=2; x=2*2=4 (было бы странно так писАть там, ибо это могло казаться бредом сумасшедшего, здесь после более общего примера хоть какое-то объяснение этому явлению)

Аналогично,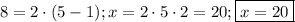 $8=2\cdot(5-1); x=2 \cdot5 \cdot 2=20; \boxed{x=20}$

И ещё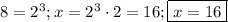 $8=2^3; x=2^3\cdot2=16; \boxed{x=16}$

ответ: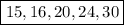 $\boxed{15,16,20,24,30}$

в) сразу пробуем 12+1=13; 13 - простое число, значит, это корень.

$\boxed{x=13}$

$(13;2)=1 \Rightarrow x=13\cdot2=26; \boxed{x=26}$

Теперь раскладываем:

$13=(3-1)(7-1); x=3\cdot7=21; \boxed{x=21}$

$(21;2)=1 \Rightarrow x=21\cdot2=42; \boxed{x=42}$

$12=2\cdot3\cdot(3-1); x=2\cdot3^2\cdot2=36; \boxed{x=36}$

$12=2\cdot(7-1); x=2\cdot7\cdot2=28; \boxed{x=28}$

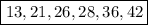
ответ: $\boxed{13,21,26,28,36,42}$

г) вот тут самое интересное. Везде, где было что простое число есть в разложении правой части без вычета единицы, это была либо 2, либо там был вид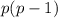 p(p-1) . 14 так не разложить

Можно лишь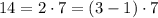 $14=2\cdot7= (3-1)\cdot7$

Можно, конечно, попытаться по "алгоритму" найти корни

$x=2\cdot7\cdot2=28;$ - этот корень к пункту в) относится, значит, не сюда точно

$x=3\cdot7=21$ - это так же к пункту в) относится. 7 представить как (8-1) нельзя, так как 8 не является простым числом. Поэтому больше вариантов нет и, соответственно, тут нет корней.

ответ: $\boxed{\varnothing}$

P.S. какую-то теоретическую информацию можно найти в книге Бухштаба. Теория чисел". В главе про функцию Эйлера, но про решение таких уравнений там нет ничего. Вообще информации про это очень мало, так что на что-то более-менее официальное рассчитывать не приходится. Надеюсь, мое решение оправдает Ваши ожидания. Корни, естественно, проверялись.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика