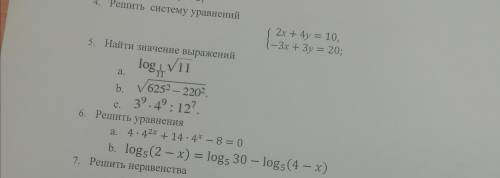
Математика: Решите уравнения А. 4*4^2x+14*4x-8=0 B. log_5(2-x) =log_5 30-log_5 (4-x)

Решите уравнения
А. 44^2x+144x-8=0
B. log_5(2-x) =log_5 30-log_5 (4-x)

Решите уравнения А. 4*4^2x+14*4x-8=0 B. log_5(2-x) =log_5 30-log_5 (4-x)

Ответы

sooooooos1 25.11.2021 05:24

Пошаговое объяснение:

для логарифмов используем

$\displaystyle log_{\displaystyle a^k}=\frac{1}{k} log_ab\\\\log_ab^m=mlog_ab\\\\log_aa=1\\\\log_a\frac{b}{c} =log_ab-log_ac$

для степеней используем

a²-b² = (a-b)(a+b)

$\displaystyle a^m*a^n = a^{m+n}\\\\(a*b)^m = a^m*b^m\\\\\frac{a^m}{a^n} =a^{m-n}\\\\a^m*b^m=(a*b)^m$

$\displaystyle log_{\displaystyle \frac{1}{11} } \sqrt{11} = log_{\displaystyle11^{-1}} 11^{\displaystyle1/2} =(-1)*\frac{1}{2} log_{11}11= -0.5\\$

$\displaystyle \sqrt{625^2-220^2} =\sqrt{(625-220)(625+220)} =\sqrt{5*81*5*169} =5*9*13=585$

$\displaystyle \frac{3^9*4^9}{12^7} =\frac{12^9}{12^7} =12^2=144$

$\displaystyle 4*4^{2x}+14*4^x-8=0\\\\4^x=z\\4z^2 +14z-8=0\\\\z_1= -4 \qquad z_2=0.5$

корень z₁ = -4 нам не подходит, т.к. у² не может быть отрицательным

тогда

$\displaystyle y^2=\frac{1}{2} \\\\y=\pm\frac{1}{\sqrt{2} } =\pm\frac{\sqrt{2} }{2}$

$\displaystyle log_5(2-x)=log_530-log_5(4-x)\\\\log_5(2-x) = log_5\bigg (\frac{30}{4-x } \bigg )\\\\2-x = \frac{30}{4-x} \\\\(2-x)(4-x)-30=0\\\\x^2 -6x -22 =0\quad x_1 = 3+\sqrt{31} \quad x_2=3-\sqrt{31} \\\\$

теперь оба корня подставляем и проверяем решение

$x=3-\sqrt{31} \\\\\displaystyle \frac{ln(2-x)}{ln5} =\frac{ln(2-(3-\sqrt{31}) }{ln5} \approx 0.94\\\\\frac{ln(30)}{ln(5) } -\frac{ln(4-x)}{ln(5)} = \frac{ln(4-(3-\sqrt{31} )}{ln(5)} =\frac{ln(\sqrt{31}-1) }{ln(5)} \approx 0.94$

это решение верное

$\displaystyle\\x= 3+\sqrt{31} \\\\\frac{ln(2-x)}{ln(5)} = \frac{ln(2-(3+\sqrt{31}) )}{ln(5) } = \frac{ln(-1-\sqrt{31} )}{ln(5)} =1.2+1.9i\pi\\\\\frac{ln(30)}{ln(5)} - \frac{ln(4-x)}{ln(5) }= \frac{ln(30)}{ln(5)} -\frac{ln(4-(3+\sqrt{31} ))}{ln(5) } =1.2-1.9i\pi$