Решите уравнение в целых числах х^2=3y^2+10
Другие вопросы по теме Математика
Популярные вопросы
- Значение выражения 7 · 1296^57 – 8 · 216^30 + 35 записали в системе...
3 - Клиент взял некоторую сумму в кредит в банке под 50% годовых. Проценты...
3 - Из предложения выпишите словосочетание, образованное на основе согласования....
2 - Яку з названих посад не обіймав Наполеон бонапарт...
2 - Переведите текст Part I. Introduction to Business Organization If...
1 - Источник испускает электромагнитные волны, длина которых 2*10^-9 м...
2 - Затопило квартиру у соседей,отключили все электричество. Сколько ждать...
2 - Определите массу хлорида бария и обьем воды, необходимые для приготовления...
2 - решить фізику: Визначиьи магнітний потік, що пронизує площадку зі...
2 - Скрипач закончил. Синтаксический разбор...
3
Рассмотрим два случая:
1). четно.
четно.
Представим число в виде
в виде 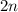 . Понятно, что сумма четного числа и еще одного четного - четная. Поэтому
. Понятно, что сумма четного числа и еще одного четного - четная. Поэтому  - тоже четное. Заменим его на
- тоже четное. Заменим его на  . Подставляем:
. Подставляем:
Но это противоречие! на
на  нацело не делится.
нацело не делится.
2). нечетно.
нечетно.
Пусть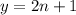 , а
, а  - нечетное - это
- нечетное - это  . Подставим:
. Подставим:
Теперь видно, что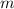 делится на
делится на  . Сделаем замену
. Сделаем замену 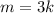 :
:
Ясно, что каждое из чисел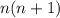 и
и  - четное (так как это произведение двух последовательных чисел). И у нас получается, что разность двух четных чисел - число нечетное (
- четное (так как это произведение двух последовательных чисел). И у нас получается, что разность двух четных чисел - число нечетное ( ), что весьма странно.
), что весьма странно.
Получаем, что корней у уравнения нет.
ответ: ∅ .