Решите уравнение: 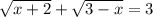
Решите неравенство:
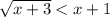
Другие вопросы по теме Математика
Популярные вопросы
- Составить ТЕХНОЛОГИЧЕСКУЮ карту сборки шкафа .Заполнить таблицу...
3 - Эллипс касается оси ординат в начале координат,а центр симметрии...
1 - Что это за аккорд в ля миноре: Соль диез, си,ре....
3 - решить задачу. Баба яга наняла Змею горыныча для оценки имеющихся...
2 - Ш.Құдайбердіұлының «Еңлік-Кебек» поэмасын трагедиямен аяқтау себебін...
3 - Мәтінмен жұмыс. Мәтінді түсініп оқы. Құстардың түрлері өте көп....
1 - В магазине имеется два бочонка сельди одного сорта. Стоимость сельди...
1 - БЫСТРЕЕ И НА ВСЕ ВОПРОСЫ ЧТО БЫ ПРАИЛЬНО БЫЛО ...
2 - Среди дробей 1/2; 5/8; 2/9; 3/5; 4/11; 1/4 выпишыте те , которые...
3 - с практической работой по математике...
2
x=2
Пошаговое объяснение:
ОДЗ: x ∈ [-2;3]
возводим обе части уравнения в квадрат, приводим подобные:
Делим обе части на 2:
возводим обе стороны в квадрат и приводим подобные:
Это II частный случай:
Решаем неравенство:
x не может быть <0, иначе корни — мнимые.
x ∈ (1; +∞)
Корень -1 не удовлетворяет условию → x=2
проверяем ОДЗ: Корень принадлежит данному интервалу → x=2