Решите уравнение.
подробно!
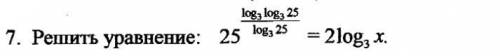
Другие вопросы по теме Математика
Популярные вопросы
- До iть будь ласка.Визначити, до якого стилю належать подані стійкі словосполучення,...
2 - Есть ли в Германии журналы только с филвордами на русском языке?...
1 - Оцінка фізико-географічну характеристику львівщини щодо її господарського...
1 - Утворіть з поданих слів деєслова доконаного виду розвивати скачувати копати...
2 - 2. Составить блок схему Найти х x=2a+2в+y, где a=2м, в = c + т y= 2/t 3....
2 - 2. 3 ясуйте, яким членом речення є виділені слова (цифра позначає наступне...
2 - Знайти екстремуми функції ...
3 - Виберіть формули гідростів оксидів які відповідають оксидам FeO...
2 - Решить , если С: z=(1-i)t, 0 =t =1...
3 - 1 построить пирамиду по точкам 2 площадь треугольника в осн этой пирамиды3...
2
(см. объяснение)
Пошаговое объяснение:
Заметим, что:
Тогда:
Данный корень удовлетворяет условию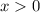 .
.
Задание выполнено!
По правилу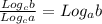 преобразуем степень числа 25.
преобразуем степень числа 25.
Получим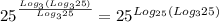 .
.
По основному логарифмическому тождеству( есть в инете)
Тогда уравнение примет вид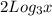 =
=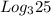 ,
,
x=5, 5>0
ответ х=5