1. Математика
  2. Решите уравнение. Математика

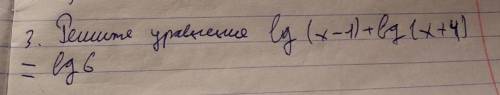
Решите уравнение. Математика 9-10 класс​


Решите уравнение. Математика 9-10 класс​

Batanik17 Batanik17    1   29.06.2021 21:23    0

Ответы
Sveta1314 Sveta1314  29.07.2021 21:57

ответ: 2

lg(x-1)+lg(x+4)=lg\;6\\ \\ lg(x-1)(x+4)=lg\;6\\ \\ (x-1)(x+4)=6\\ \\ x^2+3x-10=0\\\\\sqrt{D}=\sqrt{3^2-4\cdot 1\cdot(-10)}=\sqrt{9+40}=\sqrt{49}=7\\ \\ x_1=\dfrac{-3-7}{2}=-5\\\\ x_2=\dfrac{-3+7}{2}=2

Проверка:

x_1=-5:\\\\lg(-5-1)+lg(-5+4)=lg\;6\\ \\lg(-6)+lg(-1)=lg\;6\\ \\

Оба десятичных логарифма в левой части уравнения не существуют, так как подлогарифмическое выражение отрицательно.

Следовательно, x₁ -- посторонний корень

x_2=2:\\\\lg(2-1)+lg(2+4)=lg\;6\\ \\lg\;1+lg\;6=lg\;6\\ \\0+lg\;6=lg\;6\\ \\lg\;6=lg\;6

Верно. Следовательно, x₂ -- корень уравнения

ПОКАЗАТЬ ОТВЕТЫ
Demonis666 Demonis666  29.07.2021 21:57

x=2

Пошаговое объяснение:

lg(x-1)+Lg(x+4)=Lg6 ограничения \left \{ {{x-10} \atop {x+40}} \right. ,\left \{ {{x1} \atop {x-4}} \right. ⇒ x>1

lg(x-1)(x+4)=Lg6

(x-1)(x+4)=6

x²+3x-4=6

x²+3x-10=0 , по т.виета x₁+x₂=-3  ,x₁*x₂=-10  ⇒  

x₁= -5 не подходит тк-5<1 ,x₂=2 корень тк 2>1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
sts23 sts23  21.01.2021 10:24
МАТЕМАТИКА В ЖИЗНИ 1 Реши задачу.Безопасное расстояние между двумя автомобилями в гололёдвысчитывают по правилу: Скорость машины умножается на дваи получается дистанция в метрах. Например,...
Эммикэт Эммикэт  21.01.2021 10:24
MN - средняя линия треугольника ABC, параллельная стороне AB. Точки пересечения медиан треугольника AMN и высот треугольника ABC совпадают. Найди угол при вершине B треугольника ABC....
anya12345678900 anya12345678900  21.01.2021 10:23
Корсетилген олшем бирликтерине орнекте 8кг= ? г 8кг 558г = ? г 9г = ? мг 14кг40г=? г 256кг =? г 4г 3мг=? мг 10кг687г=?г 35кг= ? г 3г 30мг=?мг...
reginasachtova reginasachtova  21.01.2021 10:23
827. 1) |x – 4|=2 2) |y + 5| = 3;3) |3 + x|= 1,5;4) |7 – y| = -2;5) |х +3|+4 = 9;6) |y – 2| +8 = 5.​...
юська3 юська3  21.01.2021 10:23
решить примеры, по математике,...
Rifik Rifik  21.01.2021 10:23
Три предпринимателя создали акционерное общество. Первый внёс в уставной капитал 110 000 р., второй — 100 000 р., а третий — 90 000 р. Через год они получили 345 000 р. прибыли. Какони...
ГрознаяВафля ГрознаяВафля  21.01.2021 10:23
ТВОРЧЕСКАЯ РАБОТА 5Рассмотри схему.Составь задачу.V. = 16 км/чS,S=? км1Реши её.t= 4 чv, = 25 км/чS,2...
liza7634578 liza7634578  21.01.2021 10:23
сделать математику нужно. Все задания нужно сделать. Напишите...
kostyuchkova12 kostyuchkova12  21.01.2021 10:23
Решить по теореме синуса и косинуса​...
kamila285 kamila285  21.01.2021 10:23
На каждый час делать таблицу...

Популярные вопросы