Решите уравнение дифференциальное
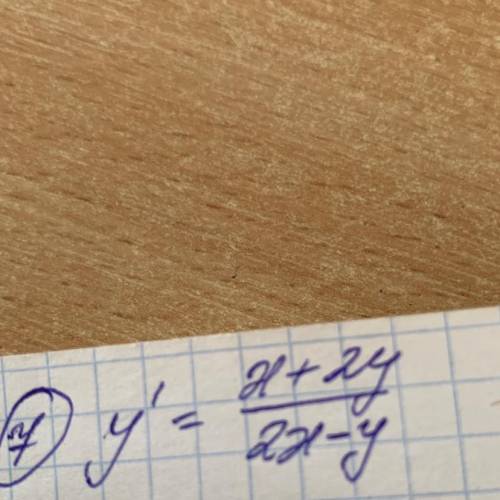
Другие вопросы по теме Математика
Популярные вопросы
- Периметр рівнобедреного трикутника дорівнює 80 см, а висота, проведена...
2 - Вслове поджигает сколько орфограм...
1 - Вцилиндрический сосуд площадью основания 100см^2 налили 1л воды...
1 - 4. сосчитайте, сколько лет назад: а) со- стоялась невская битва;...
3 - Счем реагирует этанол,пропановая кислота ,метилбутаноат...
3 - Написать небольшую творческую работу. один день из жизни митрофанушки...
3 - Мини-очерк на тему «если я туристический работник» (5-7 предложений)....
2 - древних веков 6 класс, конспект по параграфу 6автор...
1 - Управильній трикутній піраміді бічне ребро дорівнює 4√3 см і утворює...
3 - Тудын тудын тудын тун деген тауып беріндерш аты қалай детективтарда...
3
это линейное ДУ
Замена:
общее решение