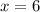Решите уравнение: 3/x^2-6x+9=1/x+3-6/9-x^2 только , если можно,
Другие вопросы по теме Математика
Популярные вопросы
- ответь на 6 вопросов по стихотворения ....
2 - Опишите события 1783-1797 года – заполнив таблицу причины руководители восстания...
2 - Логические преобразования информации M = (C imp not B and C eqv A ) А...
1 - 2-тапсырма 74 беттегі 5 тапсырма. Берілген кәсіби сөздерді пайдаланып 6-7сөйлем...
2 - Напишите кластер про Калыка Акиева...
2 - Докажите что произведение А.С.Пушкина сказка о мертвой царевне и о семи богатырях...
2 - Определи замену с которой уравнение -11х^4+2х^2-4=0 можно привести к квадрату...
2 - Төмендегі берілген кіріспе сөздерді кестеге түсір...
2 - Реформи 60-80 років 19 ст їхні значення для українського народу...
1 - Катер проплыл 6 по течению реки 8 часов против течения реки переменная. Выражение...
3
x≠3 U x=-3
3(x+3)=(x-3)²+6(x-3)
3x+9=x²-6x+9+6x-18
x²-9-3x-9=0
x²-3x-18=0
x1+x2=3 U x18x2=-18
x1=-3 не удов усл
x2=6
6
Пошаговое объяснение:
Найдем ОДЗ: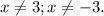
Умножим обе части уравнения на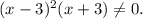
x= - з не удовлетворяет ОДЗ.
Значит, x=6 - корень уравнения.
Найдём общий знаменатель дробей:
Теперь обе части уравнения мы умножим на их знаменатель:
Обязательно вернёмся к ОДЗ (область допустимых значений):
ответ: