Решите систему уравнений (на фото)
А) по формулам Крамера
Б) методом Гаусса
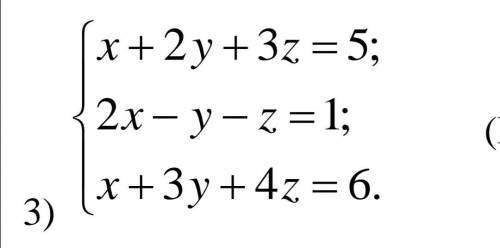
Другие вопросы по теме Математика
Популярные вопросы
- Обчисліть масу солі й об єм води для приготування 6% (0,06) розчину масою 12г...
2 - Установіть відповідність Відокремлений член речення Приклади: Все інше на фото....
3 - Домашня робота Заповнити таблицю Ознаки реального світу Ознаки уявного світу до...
2 - Х⁶-у⁶ розкладіть на множники...
3 - Поставте іменники, наведені у дужках, у потрібному відмінку. Підсунути (стілець),...
3 - Сделайте очень нужно, буду вам очень благодарна, с объяснениями. ...
1 - 5 - 9 классы Русский язык 5+3 б ТЕСТ 13 Вариант 3 Вариант 4 А. Укажите номера слов,...
3 - Якої байки Л. Глібова стосується таке прислів я: “Без труда – нема плода?...
1 - Что характерно для Фергано Ташкентских макомов? a) песенное творчество женщин и...
1 - Буду очень признателен, если Это физика: 1. Який вантаж можна підняти приклавши...
2
Давайте начнем с решения этой системы уравнений по формулам Крамера, а затем решим ее методом Гаусса.
1) Решение системы уравнений по формулам Крамера:
Для начала давайте найдем определитель матрицы коэффициентов `D` системы уравнений. Для этого составим матрицу коэффициентов:
```
2 -3
3 4
```
Определитель `D` равен `2 * 4 - (-3) * 3`, что равно `8 + 9`, то есть `17`.
Теперь найдем определители `Dx` и `Dy` для нахождения значений `x` и `y`:
Заменим первый столбец в матрице коэффициентов на столбец свободных членов системы уравнений:
```
5 -3
8 4
```
Определитель `Dx` равен `5 * 4 - (-3) * 8`, что равно `20 + 24`, или `44`.
Заменим второй столбец в матрице коэффициентов на столбец свободных членов системы уравнений:
```
2 5
3 8
```
Определитель `Dy` равен `2 * 8 - 5 * 3`, что равно `16 - 15`, то есть `1`.
Теперь найдем значения `x` и `y`, используя формулы Крамера:
```
x = Dx / D = 44 / 17
y = Dy / D = 1 / 17
```
Получаем окончательный ответ:
```
x ≈ 2.59
y ≈ 0.06
```
Таким образом, решение системы уравнений по формулам Крамера состоит в том, что `x` приближенно равно 2.59, а `y` приближенно равно 0.06.
2) Решение системы уравнений методом Гаусса:
Применим метод Гаусса для коэффициентной матрицы расширенной системы уравнений:
```
2 -3 | 5
3 4 | 8
```
Шаг 1: Домножим первую строку на 3 и вычтем из второй строки, чтобы избавиться от первого элемента второй строки:
```
2 -3 | 5
0 13 | -7
```
Шаг 2: Разделим вторую строку на 13, чтобы получить единичный коэффициент перед `y`:
```
2 -3 | 5
0 1 | -7/13
```
Шаг 3: Домножим вторую строку на 3 и прибавим к первой строке, чтобы избавиться от коэффициента `-3` в первой строке:
```
2 0 | 5 - 3*(-7/13)
0 1 | -7/13
```
Шаг 4: Разделим первую строку на 2, чтобы получить единичный коэффициент перед `x`:
```
1 0 | (5 - 3*(-7/13))/2
0 1 | -7/13
```
Таким образом, получаем:
```
x = (65/13 + 21/13)/2 = 86/26 = 43/13 ≈ 3.31
y = -7/13
```
Решение системы уравнений методом Гаусса: `x` приближенно равно 3.31, а `y` точно равно `-7/13`.
Надеюсь, я смог объяснить решение системы уравнений достаточно подробно и понятно! Если у вас возникли еще вопросы, не стесняйтесь задавать!