Решите систему уравнений:
5x+3y=1
3x-2y=1
Другие вопросы по теме Математика
Популярные вопросы
- Знайдiть суму довжин трьох вимiрiв прямокутного параллелепiпеда,...
1 - Рассказ Ю. Казакова Голубое и Зеленое от ...
3 - Адже матінка недурно казали, що не без добрих людей. Чому воно...
2 - Фотографию размером 1024*512 пикселей сохранили в виде несжатого...
3 - 4х+7 -5+х с решением :)...
2 - Привет с задачами, буду очень благодарен...
1 - 1) перепишите текст, раскрывая скобки, вставляя, где это необходимо,...
3 - −3/4⋅|x|+11,5=−2. ответ: x1= x2=...
2 - Наведіть програмний код, що змінить колір межі автофігури на...
3 - Назвати 10 « гарячих точок» планети на різних континентах (...
2
Пошаговое объяснение:
Решим систему сложения. Для этого первое уравнение умножим на 2, второе на 3 и сложим полученные уравнения.
Значит,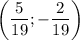 - решение системы.
- решение системы.