Решите систему уравнений
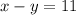
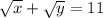

Другие вопросы по теме Математика
Популярные вопросы
- 3. Прочитайте текст. Какова его тема, тип речи? Определите стиль и тип речи....
1 - 1. доставьте «Фишбоун», используя тексты урока. Язык – самоевыразительное,ВЫВОДчем...
2 - На весах уравновешены две гири алюминиевая и медная.Какая гиря перевесит...
3 - Изложение 6 класс русский язык Город-герой Минск...
1 - Напишите выражение для нахождения объема куба, используя V=a”. Полученный...
1 - 1-тапсырма.Сұрақтарға жауап беріңдер. Салықсалғанда соғыстан кейінгі жағдай...
3 - Раздели 311745÷502 столбиком...
2 - В 280г воды растворили 30г соли. вычислите массовую долю соли в получившемся...
3 - Жазылым 10-тапсырма. «Қос жазба» күнделігі. Мәтін мазмұны бойыша берілген...
1 - потребителя сопротивлением 50 Ом и 16 ом соединены последовательно который...
3
Пошаговое объяснение:
(36, 25)
Пошаговое объяснение: