Решите ) Решение более объективней и раскрыто

Пошаговое объяснение:

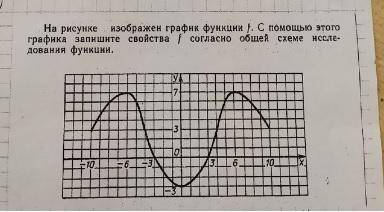
1.Четность/нечетность

Функция четна, так как симметричная относительно нуля. Это легко проверить так как f(-x) = f(x).

2. Периодичность

Функция f(x) называется периодической с периодом , если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

Такого на графике не наблюдается, значит функция непериодична.

3. Монотонность(возрастание и убывание)

Функция возрастает на интервалах (-10;-6), (0;6). Функция убывает на интервалах (-6;0),(6;10).

4. Экстремумы

Точка Хmax называется точкой максимума выполнено неравенство f(х) f(Xmax). Аналогично для минимума.

Функция имеет две точки максимума это точки -6 и 6, и одну точку минимума это 0.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

Нули функции это точки 3 и -2