1. Математика
  2. Решите ребус: АХ*УХ=2001 (разные

Решите ребус: АХ*УХ=2001 (разные буквы шифруют разные цифры, а одинаковые буквы одинаковые цифры)

НадеждаАрико НадеждаАрико    1   08.07.2021 01:19    5

Ответы
holoyf holoyf  07.08.2021 01:45

Оба двухзначных числа оканчиваются на одну и ту же цифру (пересказал условие, хех). Произведение двух таких чисел может оканчиваться на 1, если они оканчиваются либо на 1, либо на 9.

Разложим число 2001 на множители. Сразу бросается в глаза, что оно делится на 3:

2001:3=667.

Разложим 667 на множители. Тут я считерю и воспользуюсь калькулятором, получается 23*29 — это простые числа. Я не знаю, как факторизовать их без калькулятора, кроме метода перебора.

То есть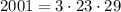 2001=3 \cdot 23 \cdot 29. Есть два варианта сделать два двухзначных числа:

(3 \cdot 23) \cdot 29=69 \cdot 29 — последние цифры одинаковы, подходит.

(3 \cdot 29) \cdot 23=87 \cdot 23 — последние цифры одинаковы, не подходит.

ответ: 69 \cdot 29.

P. S. Возможно, перейдя к десятичному представлению чисел и найдя там какие-то закономерности, можно решить проще без калькулятора. Попробуйте:

\overline{AX} \cdot \overline{YX}=2001\\\overline{A1} \cdot \overline{Y1}=2001\\(10A+1)(10Y+1)=2001

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
baryshnikova20 baryshnikova20  05.04.2020 04:23
ответьте как сделать минус 5/6-1/4=...
margaritakulak margaritakulak  05.04.2020 04:22
Определи: является ли корнем уравнения 2x+5=17 число 9?...
isheh09ow2mth isheh09ow2mth  05.04.2020 04:24
Выберите правильный ответ.Какой знак имеет корень уравнения3x+4=5−2x3x+4=5−2x​...
jernova jernova  05.04.2020 04:23
Деревянный брус размером 10см*10см*200см распилили на одинаковые пластины для паркета. Каждая пластина имеет размер 1см*5см*20см. Сколько пластин получилось из этого бруса Очень...
Aliotu Aliotu  05.04.2020 04:24
На рисунке изображены мать и сын. Рост сына — 101 см. Найди примерный рост матери (на рисунке сын примерно в 1,3 раза ниже матери). ответ дай в сантиметрах, округлив до целых....
Diifekt Diifekt  05.04.2020 04:24
Чему равен объем прямоугольного параллелепипеда с площадью основания 20 см² и высотой 4 см варианты ответов80 см²120 см²60 см²​...
2007628475626 2007628475626  05.04.2020 04:25
Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 385 рублей. Вторая семья купила три детских билета и два взрослых...
killbestrong killbestrong  26.06.2019 20:10
Решить 50+4•х=82 и 3•(х+6)-23=16 !...
альбинка28 альбинка28  26.06.2019 20:10
Покажите, что числа являются рациональными: 0,85 -3,4 -1 целая 3/8 5 целых 5/6 12. заранее 80 за правильное !...
SofaI SofaI  26.06.2019 20:10
Используя калькулятор, определи на сколько нужно уменьшить число 387921, что бы получить число, которое нацело делится на число 95. найди три варианта ответа....

Популярные вопросы