Решите : ребро куба в 2 1/6раза больше ребра другого куба. во сколько раз отличаются их площади?

Ответы

Nikita45Nikita45 23.06.2020 09:23

ответ: Площади куба отличаются в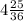 $4\frac{25}{36}$ раз.

Пошаговое объяснение:

Площадь куба вычисляется по формуле:

$S = 6*x^{2}$

Считаем площадь первого и второго кубов:

$S_{1}=6*x^{2}\\S_{2}=6*(2\frac{1}{6}x)^{2}=6*( \frac{13}{6})^{2}* x^{2}=\\6*\frac{169}{36}x^{2}=\frac{1014}{36} x^{2}=28\frac{1}{6} x^{2}$

Теперь делим площадь первого куба на площадь второго:

$\frac{28\frac{1}{6}x^{2}}{6x^{2}}=28\frac{1}{6}:6=\frac{169}{6}:\frac{6}{1}=\frac{169}{6}*\frac{1}{6}=\frac{169}{36}=4\frac{25}{36}=4\frac{25}{36}$

ответ немного переправил, была небольшая опечатка

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Ученица950 20.05.2021 09:02

kostrominalekceu 20.05.2021 09:02

Памагите с контрольной 7, 8,9...

Maxyim 20.05.2021 09:02

Что вы знаете об абсулютизме...

Redll 20.05.2021 09:01

Щкх 20.05.2021 08:59

Victor111111111 20.05.2021 08:57

ПОЖ С ПРИМЕРОМ ) − 3,4 − = −4,3...

BonYseT 20.05.2021 08:56

def04565 20.05.2020 07:02

Сравните числа: А) 0,7921 и 0,7917 б) - 3/7 и -0,2...

kokbhj 20.05.2020 07:02

Kvasya07 20.05.2020 07:02

написать соч по Математики. У меня 30 мин....