Решите полностью, там вроде должно все сократиться,
Другие вопросы по теме Математика
Популярные вопросы
- Впространстве, где существуют однородные постоянные магнитные и электрическое...
3 - Вычислите значение выражения: (y−347)⋅x если x=19,y=63...
3 - Превысит слово самолёт на франсуский...
2 - Дан пример 1234-(89747-6753)×3+388675=...
3 - 2. странный месяц в некотором месяце первый день и средний день пришлись на...
2 - 1. кто такие клюнийцы и каких целей они добивались всемирная...
1 - Впредложение , на зелёных. свежих. ветках . есть ли прилагательные...
2 - Ab=4,2см.bc=8,4см. найти: угол b ну вас! прям нужно!...
1 - Вычислить значения выражения : 125целых 2/3+25целых 3/2+корень из 16 .(подробные...
3 - Услова красный несколько значений. , два самых популярных - это 1.красивый...
1
Сделаем замену:![\sqrt[3]{8}=u,\; \sqrt[3]{5}=v](/tpl/images/1073/3491/11f1f.png) ;
;
Имеем: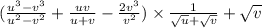 ; В скобках:
; В скобках: