Решите показательные уравнения
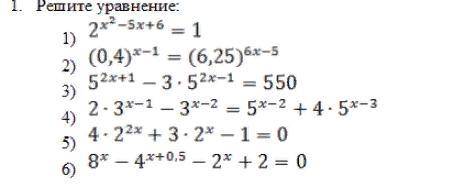
Другие вопросы по теме Математика
Популярные вопросы
- До ть будь ласка, треба над кожним словом у вправах написати...
2 - Сколько всего городов в штате Флорида в США? ...
1 - 312. Составьте и запишите отдельные предложения или небольшой...
2 - на картинке два вопроса ответьте на них ...
2 - Крупный город вблизи Такомы на северо-западе США, какой именно?...
2 - Письмо очумелову по чехову хамелеон...
2 - Самый экологически чистый регион России, что это за регион?...
3 - Какое государство в истории человечества впервые применила...
2 - Прокомментируйте подчеркнутое предложение раскрыв значение слова...
1 - If you worked more quickly, you be able to go home earlier.1)`ll...
1
ответ: 2,3.
Замена:
нет корней.
ответ:-2.
Замена:
корень -1 не подходит.
ответ: 0;1.