Решите параметр №18 из ЕГЭ
( )

(см. объяснение)

Пошаговое объяснение:

, ОДЗ: .

Заметим, что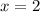 является корнем уравнения при любом значении параметра. Тогда нужно, чтобы уравнение имело ровно один корень принадлежащий ОДЗ и не равный двум.

Введем замену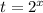 . Откуда .

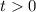Тогда уравнение примет вид:

Переформулируем условие задачи:

Найти все значение параметра , при каждом из которых записанное выше уравнение имеет ровно один корень, принадлежащий промежутку .

Введем функцию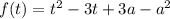 . Это парабола, ветви которой направлены вверх, а координата вершины имеет значение .

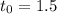Отрисовав возможные расположения парабол, учитывая расположение ее вершины, перейдем к системам:

(я рисовать их не буду, так как на компьютере это неудобно + вы говорите, что уже сами задачу решили)

         /или/          

Выполним необходимые вычисления:

Тогда записи примут вид:

         /или/    

Итого при исходное уравнение имеет ровно два различных корня.

Задание выполнено!