Решите неравенство 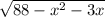 +x^3-7x ≤
+x^3-7x ≤ 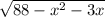 +3x+9x^2.
+3x+9x^2.
Другие вопросы по теме Математика
Популярные вопросы
- Сколько бит информации в 4 Мбайт?...
2 - Почему по Вашему мнению Роман Дефо получил такую широкую известность...
3 - Из своих норок одновременно навстречу друг другу выбежали мышата Бим...
3 - Что необходимо для создания мультфильма? Предложите свой сценарий для...
1 - В чем биологический смысл загара?...
2 - На какого сказочного персонажа напоминает Ваня Солнцев из повести сын...
2 - Тринадцатый подвиг Геракла найти и объяснить в этом произведении черты...
3 - Какой вклад в изучение Евразии внесли такие исследователи как: …Марко...
3 - ответить на во теста Тест до твору Сiроманець 1. Кого вовк вичiкував...
1 - Перечислите закономерности географической оболочки...
3
х∈[-11;-1]∪[0;8]
Пошаговое объяснение:
1)
Решаем методом интервалов, найдём корни кв. урвавнения по теореме Виета :х₁=10 и х₂=-1 и корень х=0
____________________-1______0_______________10_______
- + - +
x∈(--∞;-1]∪[0;10]
___-11__________________________________ 8_________
+ - +
Выпишем общее решение:
х∈[-11;-1]∪[0;8]