Решите неравенство методом интервалов: (4x-1)/(3x+1)≥1.

Пошаговое объяснение:

(4x-1)/(3x+1)≥1.

Равносильно (х-2)(3х+1)≥0 при х≠-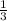   . Метод интервалов :

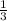+++++(-)----------[2]++++++++, х∈ (-∞;-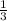) и [2;+∞)

ответ: см фото. Диапазон от минус бесконечности до -1/3 (не вкл) и от 2 до плюс бесконечности.

Пошаговое объяснение: