1. Математика
  2. Решите неравенство log^2(1-2x)

Решите неравенство log^2(1-2x)> 0

kotik53Tv kotik53Tv    1   31.07.2019 07:00    1

Ответы
imailh28282 imailh28282  28.09.2020 13:03
Любое выражение в квадрате неотрицательно, то есть либо положительно, либо ноль. Если рассматривается неравенство, где записан  строгий знак Х²>0, то  Х может быть как положительным (Х>0), так и отрицательным (Х<0) , но не может быть нулём. 

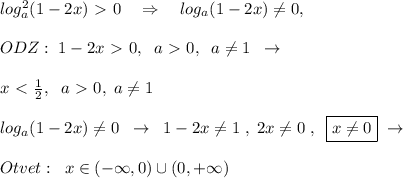
log^2_{a}(1-2x)\ \textgreater \ 0\quad \Rightarrow \quad log_{a}(1-2x)\ne 0,\\\\ODZ:\; 1-2x\ \textgreater \ 0,\; \; a\ \textgreater \ 0,\; \; a\ne 1\; \; \to \\\\x\ \textless \ \frac{1}{2},\; \; a\ \textgreater \ 0,\;a\ne 1\\\\log_{a}(1-2x)\ne 0\; \; \to \; \; 1-2x\ne 1\; ,\; 2x\ne 0\; ,\; \; \boxed {x\ne 0}\; \to\\\\Otvet:\; \; x\in (-\infty ,0)\cup (0,+\infty )
ПОКАЗАТЬ ОТВЕТЫ
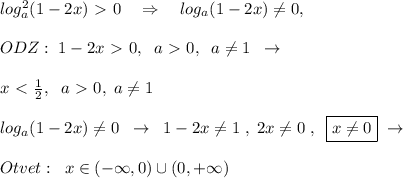
Другие вопросы по теме Математика
Ddoj Ddoj  26.09.2019 22:20
Ущенят и утят вместе 50 ног и 20 голов. сколько утят?...
alex12345lex alex12345lex  26.09.2019 22:20
Обчислити: (2 3/7: 10,2+2 2/3∙2/7)3...
DariaMejor DariaMejor  26.09.2019 22:20
Три курицы за 3 дня снесли 3 яйца. сколько яиц снесут 30 куриц за 30 дней, если они будут нестись с такой же производительностью?...
HasteBro HasteBro  26.09.2019 20:54
Нужно решить лёгкое ! можно без объяснения, просто !...
MissEvaStar MissEvaStar  26.09.2019 22:20
Высота конуса равна 15, а диаметр основания 20. найти образующую конуса....
sigaretta sigaretta  26.09.2019 20:54
Решите систему неравенств, ❤️ надо, люди добрые...
yancenkostya yancenkostya  26.09.2019 22:20
Решение логарифмов lg(√2) * log(10)по основанию 2...
m3rry1 m3rry1  26.09.2019 22:20
Толик грав в компютерну игру повтори години ,потим ще чверть години й 3 хв.сколько секунд толик игра в в компютерну гру ?...
Siruk217 Siruk217  26.09.2019 22:20
Найди площадь заштрихованной фигуры 14 см длина 5 см ширина внутри прямоугольник 4см длинп и 3см ширина надо найти площадь 14 и 5 на считая прямоугольника внутри...
Awesome7 Awesome7  26.09.2019 22:20
Решить тригонометрическое . уравнение 2tg x= -3 а) имеет одно решение б) имеет множество решений в) имеет два решения г) имеет бесконечное множество решений....

Популярные вопросы