Решите неравенства
1. sin x/2 cos x/2 больше 1/2
карточка
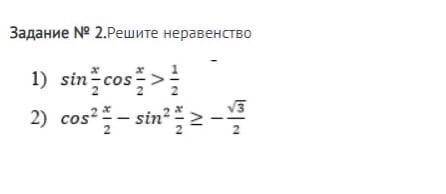
Другие вопросы по теме Математика
Популярные вопросы
- Трудовой договор закрепляет договорной характер трудовых правоотношений, свободу,...
2 - К документам, которые представляются инвалидом в орган службы занятости для...
3 - В течение одного месяца (другого учетного периода) продолжительность рабочего...
3 - В течение учебного года продолжительность еженедельного и ежедневного рабочего...
2 - Предметом изучения дисциплины Технологии профессионально-ориентированного обучения...
1 - Число студентов в группе ограничивается при проведении практического занятия...
3 - Прогул означает отсутствие на рабочем месте без уважительных причин в течение...
1 - Период временной нетрудо работника и другие периоды, когда он фактически отсутствовал...
2 - Древнерусский язык унаследовал в Р. мн. ч. для разных склонений три флексии:...
3 - К дополнительным основаниям прекращения трудового договора с руководителем организации...
2
1)
умножим на 2, чтобы слева получилась формула двойного угла.
здесь нет решения, потому что область опрелеления:
2)
собираем по формуле двойного угла косинуса
рисунок
n принадлежит Z.