Решите неполное квадратное уравнение 56х²-35х=0 4х=х²
Другие вопросы по теме Математика
Популярные вопросы
- Морфологический разбор слово без шляпы 4 класс...
2 - Напишите сочинение на тему можно ли доверять информации в интернете?...
1 - Этапы становления личности примеры адаптации индивидуализации интеграция...
1 - Перевести с на французский: переделать свою работу, зайти еще раз к своему другу,...
2 - Вкакой части евразии находится полуостров индостан ?...
3 - Как называется самый маленбкий колокольчик...
3 - Окисление nh3 осуществляет 1)нитрогеназы 2)денитрификаторы 3)нитрификаторы 4)аммонификаторы...
3 - Краткая характеристика достижений мартина лютера...
1 - Написать эссе на казахском языке про трёхязычие...
2 - Образуйте от слова канцтовары,спортбаза слова...
3
1) 56x²–35x=0;
7x(8x–5)=0;
7х=0 или 8х–5=0;
х=0 или 8х=5 => х=⅝.
ОТВЕТ: 0; ⅝.
2) 4х= х²;
х²–4х=0;
х(х–4)=0
х=0 или х–4=0;
х=0 или х=4.
ОТВЕТ: 0; 4.
Пошаговое объяснение:
56x² - 35x = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-35)² - 4·56·0 = 1225 - 0 = 1225
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ =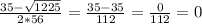
x₂ =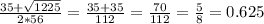
ответ: х₁=0; х₂=0.625
2) 4х=х²
переносим х² в левую часть, приравнивая уравнение к 0
-x2 + 4x = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 42 - 4·(-1)·0 = 16 - 0 = 16
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ =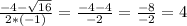
x₂ =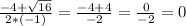
ответ: х₁=4; х₂=0