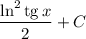Решите неопределенный интеграл
Другие вопросы по теме Математика
Популярные вопросы
- Что значит позариться? а) опозориться б)злиться в)познать злость г)смотреть...
2 - Вделении клетки выделяют: а) 4 стадии; б) 2 стадии; в) 6 стадий...
2 - Можно ли следующие объекты считать информационными моделями: *расписание уроков...
3 - Решите с уравнения (416-420). 1) в железной руде масса железа на 44 кг больше...
2 - Перед выполнением вычислений сделайте прикидку. 37 872: 72 546 455: 91 11 774:...
1 - Как сказать на в каком году появился панк рок?...
2 - Что из перечисленного имеется и у амебы, и у эвглены, и у инфузории? сократительная...
3 - Кто такая мет сестра и какие у неё качества? !...
3 - Лучше есть свой черствый хлеб, чем чужой плов. чем вам нравится эта пословица?...
1 - Когда и где был написан роман что делать...
3
Как нашли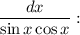
ответ: