Решите матричное уравнение с подробным объяснением
Другие вопросы по теме Математика
Популярные вопросы
- Жизнь ребёнка из семьи дворян. описать! заранее ! )...
1 - Можете составить мне 9 предложений со словом кемдер...
2 - Соедини стрелками имена князей и название материала из которого они строили...
1 - Вычислить sin острого угла если cosa=5/13...
1 - Вот решаешь-решаешь,а некоторые даже не говорят....
3 - Составить диалог со всеми этими словами : производство обуви, исследование...
1 - Обьясните как роза приручила маленького пронца?...
1 - Замените в числе 25*** звёздочки четными цифрами так, чтобы полученное...
3 - Сдокажите, что углы равностороннего треугольника равен 60 градусам...
3 - Найдите значение выражения (1,6*10^-2)*(5*10^-4) 1)0,000008 2)0,008 3)8...
2
Имеем дело с однородной СЛАУ, у которой кол-во неизвестных больше кол-ва уравнений, значит, имеем нетривиальные решения.
Приведем матрицу к ступенчатому виду:
Меняем 1 и 3 строки:
Вычитаем из второй строки первую, умноженную на 7:
Делим на -2 вторую строку и прибавляем к 3 строке первую, умноженную на 4:
Вычитаем из 3 строки вторую:
Вычитаем из 2 строки третью:
Вычитаем из 3 строки вторую, умноженную на 4:
Ранг равен трем, откуда количество свободных переменных равно 4 - 3 = 1. Пусть D - свободная переменная. Тогда
Значит,
ответ: векторы вида![\tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/1e9f9.png) , при
, при 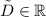 .
.