Решите маленькое уравнение
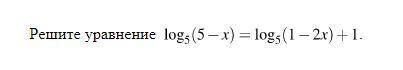
Другие вопросы по теме Математика
Популярные вопросы
- Знайдіть площу криволінійної трапеції,обмеженої лініями y = –x2 – 4x, y = 0, x...
3 - Что такое потребность? Обществознание...
2 - Какой рост у этих парней просто для интереса как думаете я потом удалю...
2 - За до карти та ее легенди зясуйте яку информацию про кимерийцив можно дизнатися...
3 - ЗАВТРА СЕССИЯ Тема: Возрождение в Европе 1. Причины Возрождения 2. Основные черты...
1 - Корень в слове марфемика-марфология...
2 - Какой ответ правильный? Границы тени точно повторяют границы освещенного объекта...
2 - нужно , от и подписываюсь...
1 - Виписати ознаки балади на прикладі балади Рибалка . Робота виконується у зошиті....
2 - Определи наибольшее значение функции y=x+2−−−−√+1 на отрезке [−2;2]. ответ: y наиб=...
1
x=0
Пошаговое объяснение:
log₅(5-x)=log₅(1-2x)+1
(log(5-x))/log5 = (log(1-2x))/log5 + 1
-1 - (log(1-2x))/log5 + (log(5-x))/log5 = 0
- (log5+log(1-2x)-log(5-x))/log5 = 0
log5+log(1-2x)-log(5-x)=0
log(5(1-2x)/5-x)=0
(5(1-2x)/(5-x)=0
5(1-2x)=5-x
5-10x=5-x
-10x+x=5-5
-9x=0
x=0
ОДЗ: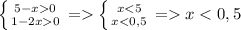
Проверка:
ответ: {0}