1. Математика
  2. Решите логарифмическое

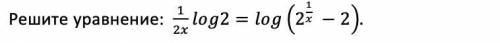
Решите логарифмическое уравнение


Решите логарифмическое уравнение

jokeaaaaff jokeaaaaff    1   28.10.2020 00:06    0

Ответы
danilohca danilohca  27.11.2020 00:06

x=\frac{1}{2}

Пошаговое объяснение:

ОДЗ:

\left\{\begin{array}{ccc}x\neq0\\\\2^{\frac{1}{x} }-20 \end{array}\right \longrightarrow\left\{\begin{array}{ccc}x\neq0\\\\2^{\frac{1}{x} }2^1 \end{array}\right \longrightarrow\left\{\begin{array}{ccc}x\neq0\\\\{\frac{1}{x} }1 \end{array}\right \longrightarrow\left\{\begin{array}{ccc}x\neq0\\\\x

Перепишем левую часть по свойству логарифма:

\frac{1}{2x}\cdot log(2)=log(2^{\frac{1}{2x}})

Приравняем подлогарифмические выражения:

log(2^{\frac{1}{2x}})=log(2^{\frac{1}{x}}-2)\\\\2^{\frac{1}{2x}}=2^{\frac{1}{x}}-2\\\\2^{\frac{1}{x}}-2^{\frac{1}{2x}}-2=0

Замена переменной: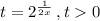  t=2^{\frac{1}{2x} } \, ,t0

t^2-t-2=0\\\\\left[\begin{array}{c}t_1=-1\\\\t_2=2\end{array}\right

В силу выбора переменной первое слагаемое не может быть решением (оно отрицательное).

Возвращаем замену:

2^{\frac{1}{2x} }=2^1\\\\{\frac{1}{2x} }=1\\\\x=\frac{1}{2}

Полученное решение удовлетворяет ОДЗ.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
вадим839 вадим839  05.10.2019 21:30
Является ли число 156 членом арифметической прогрессии (аn),в которой а1=2,а4=23...
Was1231 Was1231  05.10.2019 21:30
10*9*8*7*6*5*4*3*2*1 раставьте правильно знаки вместо звёздочек что бы получилось 2019...
1553VinyaPyhtya 1553VinyaPyhtya  05.10.2019 21:30
Решите систему уравнений {2x-7y=14 {3x+2y=-14...
KrASaVa307 KrASaVa307  05.10.2019 21:30
Найдите сумму двадцати четырех первых членов арифметической прогрессии 26,30,34...
dianadavletova dianadavletova  05.10.2019 21:30
Назовите большой круг проходящий через зенит и северный полюс мира...
Кетшити Кетшити  05.10.2019 21:30
На какое наибольшее число частей можно разрезать круглый торт семью прямолинейными разрезами? а.31 в. 29 с. 27 д. 24...
Fredbreyn Fredbreyn  05.10.2019 21:30
Пироги восемь с картошкой остальные с капустой всего 40 пирогов сколько процентов пирогов с капустой решить без x большое ❤️))...
Алена1563795 Алена1563795  05.10.2019 21:30
2sin45°-4cos30°=5sin30°-ctg45°=6ctg60°-2sin60°=...
akimhikp01b5f akimhikp01b5f  05.10.2019 21:30
Вспортивном лагере 1/5 часть прибывших туристов разместили в гостинице 1/9 часть в летних домиках. остальные 93 туриста в палатках. сколько туристов прибыло в лагерь?...
hjhytu hjhytu  05.10.2019 21:30
Какова рентабельность предприятия если было продано 10тыс.изделий по цене 5 тыс руб производство обошлось в 40млн.руб...

Популярные вопросы