Решите логарифмическое неравенство с объяснениями по ОДЗ.
Другие вопросы по теме Математика
Популярные вопросы
- Докажите неравенство b(a^2+1)+a(b^2+1) больше или равно 4ab (a больше...
2 - Решить . расстояние между пунктами а и б 384 км. из а в б выехал...
2 - Подчеркни слова, а которых буквы е, ю, я обозначают два звука. юла,...
2 - Подумай и ответь. мама испекла круглый пирог и сделала в нем три...
3 - Перетворити числовий масштаб на iменований 1: 1000; 1: 2000; 1:...
1 - Периметр треугольника bdk равен 64 см. сторона bd = 28 см , а сторона...
3 - Отличие плотной соединительной ткани от рыхлой...
2 - Подумайте и обсудите с родителями или друзьями нужны ли вообще в...
3 - Решите факториалы . 1! ×9! *5! ×5! /(1! ×4! ×0! ×5! ×10! )...
2 - Какие были придуманы указы при екатерине 2...
3
x∈(0; +∞)
Пошаговое объяснение:
Одз:
x∈(-1; 0) ∪ (0; +∞)
1) При 0< X + 1 < 1 ⇒ -1 < x < 0;
получаем отрезок:
x∈(-1; 0) (1) он соответствует нашему ОДЗ, можно не вносить правки.
Т.к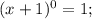 , а единица всегда меньше 2. То выражение (2) не имеет решения.
, а единица всегда меньше 2. То выражение (2) не имеет решения.
2) При X+1 > 1 ⇒ X > 0
получаем отрезок:
x∈(0; +∞) Находим пересечение с ОДЗ, которые мы нашли ранее.
x∈(0; +∞) ∩ x∈(-1; 0) ∪ (0; +∞) = x∈(0; +∞) (3)
Т.к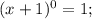 , а единица всегда меньше 2. То выражение (4) имеет бесконечное множества решений, x∈(-∞; +∞). Найдя пересечения (3) и (4) :
, а единица всегда меньше 2. То выражение (4) имеет бесконечное множества решений, x∈(-∞; +∞). Найдя пересечения (3) и (4) :
x∈(0; +∞) ∩ x∈(-∞; +∞) = x∈(0; +∞)
Мы найдем отрезок удовлетворяющий всем условием задания
ответ: x∈(0; +∞)