Решите квадратное уравнение неполным с решением
4x^2-1=0
6x^2-9=0
Другие вопросы по теме Математика
Популярные вопросы
- Які риси характеру Аліси з країни чудес виявились під час чаювання...
3 - Решите пример. х:39)+3,2×0,7=14,7...
1 - для определения высоты столба А1С1, изображенного на рисунке, использован шест...
1 - Запишите пересечение и объединение заданных интервалов чисел в числовой соли (-...
2 - Что из нижеперечисленного может являться признаком финансового мошенничества? сверхнизкий...
3 - Как решить (-10)-(-30) ? Можете объяснить ответ...
1 - по геометрии. Очень . (брэйли больше не даёт) СОЧ. ...
3 - Read these sentences and fill in the gaps with could , can , couldn t , can t ....
3 - Масса оболочки шара равна 150 кг, шар найдут гелием, объем шара - 1000 м в кубе,...
2 - У поданих реченнях знайдіть слова або вирази, що не відповідають стилістичним і...
3
ответ: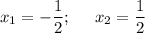
ответ: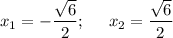
1) x = ± ½;
2) x = ± √6/2.
Пошаговое объяснение:
1)
2)