Решите , исследовать функцию(на экстремулы)
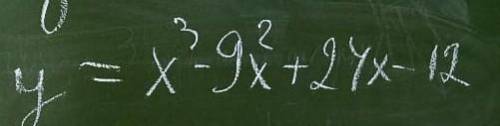
Другие вопросы по теме Математика
Популярные вопросы
- Проверь, верно ли решена задача. Исправь ошибки в столовой в первом...
3 - Давление воздуха в закрытом сосуде при температуре t1=27°С составляет...
1 - 00000000000000000000000000000...
1 - Составь текст-повествование «Новый год в Казахстане»(150 слов минимум)...
3 - Урок 73 страница 119 номер 2 3 4 класс ...
3 - Что общего в технологиях обработки металлов и пластмасс и ручными инструментами...
1 - ть будь ласка.Потрібно написати лист з привітанням з новим роком від...
2 - Определить плотность загрязнения почвы и коэффициент перехода (почва-растение)...
3 - Мой друг письмо 60-70 слов ...
3 - Определить точность метода исследования остатков токсического вещества,...
2
Пошаговое объяснение:
экстремумы функции ищем при первой производной
y'(x) = 2x² -9*2x +24
2x² -18x +24=0 ⇒ x₁ = 2; x₂ = 4 - это и есть точки экстремума
f(2) = 8
f(4) = 4
тут, в общем-то, и так понятно, где максимум а где минимум
но мы сделаем по правилам
используем достаточное условие экстремума функции. найдем вторую производную:
y''(х) = 6·x-18
смотрим знак второй производной в критических точках
y''(4) = 6 > 0 - значит точка x = 4 точка минимума функции.
y''(2) = -6 < 0 - значит точка x = 2 точка максимума функции.
ответ