Решите интегралы которые показаны на картинке
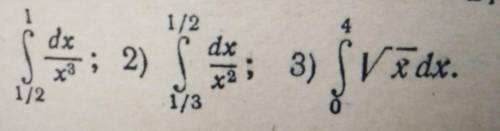
Другие вопросы по теме Математика
Популярные вопросы
- Увеличилось каждое из чисел 7,5,6,8,9 в 5 раз.уменьшилось каждое из чисел...
1 - Почему александр македонский смог завоевать огромную территорию...
2 - Составь и запиши по три-четыре слова к каждой модели корень : -лес-, дом,...
3 - Найди значения выражений a-7 и a+8 при a=23,a=57,a=60,a=92....
1 - Водин магазин 27 коробок печенья а в другой-30 таких же во 2 магазин на 24...
2 - На доске записано натуральное двухзначое число федя приписал к нему цифру...
1 - 1) запишите все целые числа больше -10 и меньше -3...
3 - Какие крылатые выражения или пословицы есть в произведении мустая карима...
1 - X=-y+3 и 3(y+1)=y+2x+4найдите сумму координат точки пересечения прямых,заданных...
3 - Как решить в составе пассажирского поезда 16 вагонов в каждом из 6 вагонов...
1
1) 3/2 = 1,5
2) 1
3) 16/3
Пошаговое объяснение:
1) ∫ 1/x³ dx = ∫ x⁻³ dx = 1/(-2) * x⁻³⁺¹ + C = -1/2 * x⁻² + C
Интегрируем в пределах от (1/2) до (1), по формуле Ньютона-Лейбница:
-1/2 * 1⁻² - ( -1/2 * (1/2)⁻² ) = -1/2 + 2 = 3/2 = 1,5
2) ∫ 1/x² dx = ∫ x⁻² dx = 1/(-1) * x⁻²⁺¹ + C = - x⁻¹ + C
Интегрируем в пределах от (1/3) до (1/2), по формуле Ньютона-Лейбница:
-(1/2)⁻¹ - (-(1/3)⁻¹) = -2 + 3 = 1
3) ∫ √x dx = ∫ x^(1/2) dx = 1/(3/2) * x^(1/2 + 1) + C = 2/3 * x^(3/2) + C
Интегрируем в пределах от (0) до (4), по формуле Ньютона-Лейбница:
2/3 * 4^(3/2) - 2/3 * 0^(3/2) = 2/3 * 2^(2* 3/2) - 0 = 2/3 * 2³ = 2/3 * 8 = 16/3
*Замечание:
В данных примерах я не стал находить определенный интеграл сразу только по техническим причинам: в предоставленной клавиатуре не существует степени (то есть знака надстрочной записи) в виде дроби(например) и многого другого.