Решите геометрию
Найти высоту, опущенную из вершины А.
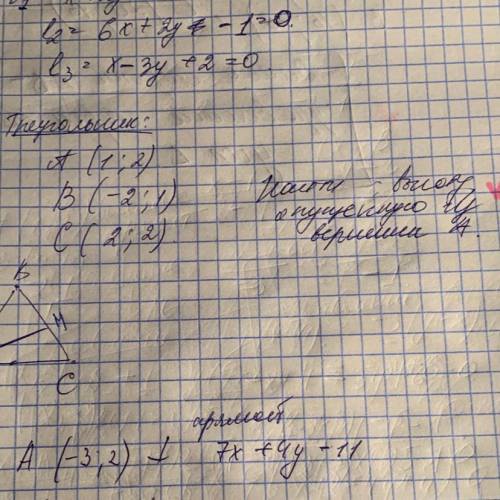
Другие вопросы по теме Математика
Популярные вопросы
- Покажите с рисунка что 3/10 дм+2/10 дм=1/2 дм...
2 - Что стало причиной значительного роста числа приказов в россии в xvii в?...
2 - Вариант 1. вычислите: /9: 6 /11÷(-25) /17÷(1) г).1÷(-9/1513701 вариант 2....
1 - Как проверить букву д в слове поздней, и как пишется в дали или вдали....
1 - Выберите лишнее. работа со списками может применяться: при составлении плана...
3 - Умальвины на клумбе росло 28 роз.11 из них она срезала для букета.сколько...
1 - Словесный портрет братьев по сказке два брата е шварц...
3 - Расстояние между двумя мотоциклистами в начале их одновременного движения...
2 - Четверостишие про весну на казахском...
2 - Подчеркните главные члены предложения.составьте схему предложения. на пятые...
2
Дан треугольник АВС. Требуется найти высоту, опущенную из вершины А.
Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов.
Используя формулу S = ½ * |a × b|, вычислим площадь данного треугольника , где а = АВ = (-2 - 2; 1 – 1; 2 – (-3)) = (-4; 0; 5) и b = АС = (2 - 2; 4 – 1; 2 – (-3)) = (0; 3; 5).
Найдем векторное произведение векторов a и b: a × b = (0; 175; 0).
Тогда |a × b| = = √(0² + 175² + 0²) = 175.
Используя формулу определения расстояния между двумя точками, вычислим длину стороны ВС.
Имеем: ВС = √((2 – (-2))² + (4 - 1)² + (2 – 2)²) = √(4² + 3² + 0²) = √(25) = 5.
Как известно, площадь треугольника равна половине произведения основания на высоту.
Следовательно, высота опущенная из вершины А равна отношению удвоенной площади на основание ВС.
Имеем 2 * 87,5 / 5 = 175 : 5 = 35.
ответ: 35.