Решите это неравенство . Подробно
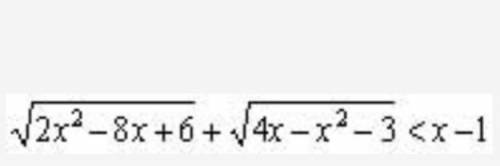
Другие вопросы по теме Математика
Популярные вопросы
- Make up and write down ten true sentences. 1) Wine2) Coffee3) Books4) Gold5)...
3 - Яким почуттям сповнений ліричний герой поеми моє серце в верховині...
1 - 5. Побудувати прямокутник площею 22 см і довжиною 11 см.Знайти периметр...
3 - Какое два оборудования нужно использовать при изучении пеницилла? СРОЯНО...
3 - 1.2. Три но изображённых объектов объединены общим признаком. Выпишите назван...
2 - Найти прямую пересечения плоскостей (B1,C,D) и (A,D,D1).Дано куб ABCDA1B1C1D1...
2 - Подивитися і виконати практичну роботу яке є у відео (((https://youtu.be/dgceBcgFTH0...
1 - Змішали 200г 5% розчину солі з 300г 10% розчину цієї ж солі. Знайти масову...
1 - Kzt , Нужно сделать 10 вопросов и 10 ответов на них, и сделать диалог с...
3 - 5. Лес, луг и пашня занимают 650 га. Из них 1 8 лес занимает всей земли,...
1
x = 3
Пошаговое объяснение:
Заменим выражение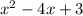 на t, тогда левая часть будет иметь вид
на t, тогда левая часть будет иметь вид
Тогда решаем уравнение t = 0
По теореме Виета легко находятся корни 1 и 3.
При x = 1:
Неравенство принимает вид 0 < 0, что не является верным неравенством.
При x = 3:
Неравенство принимает вид 0 < 2 и это является верным неравенством
3.
Пошаговое объяснение:
Найдем область допустимых значений. Так как арифметический квадратный корень определен на множестве неотрицательных чисел, то найдем ОДЗ, решив систему неравенств.
Решим отдельно каждое неравенство методом интервалов.
Рассмотрим функцию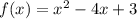
Определим знак функции на каждом интервале и получим:
Данная системе имеет решение только, если х=1 и х=3.
Проверим каждое значение:
x=1
неверно
x=3
Данное неравенство верно. Значит, решение заданного неравенства является х=3