Решите дифференциальное уравнение с разделяющимися переменными
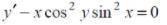
Другие вопросы по теме Математика
Популярные вопросы
- Еңлік - Кебектің идеясы мен тақырыбы...
2 - А) Запишите квадратное уравнение, если а=3, b=0, c=5 и определите...
1 - 5. С двух аэродромов, расстоя- ние между которыми 1540 км, одновременно...
3 - Функции заданы формулами f(x)=x2+1 и g(x)=x2−1. Сравни f(−6)...
3 - Составьте рекламный текст и слоган о пользе изучения биологии...
1 - , огрганічна хімія актуально в межах години!...
3 - Программа в Visual studio на С# после сохранения ехе - не открывается....
3 - Подготовить доклад про одно промышленное предприятие Казахстана....
1 - Выразите из уравнения переменную y через x:x+y=2...
1 - . Визначити середню арифметичну швидкість кисню. Молярна маса...
3
общее решение