Решите дифференциальное уравнение
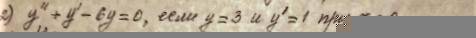
Другие вопросы по теме Математика
Популярные вопросы
- Впервой грядки собрали 16 кг капусты со второй 12 кг капусты а...
1 - Зачем были построены пирамида хеопса и статуя сфинкса...
3 - Какими членами предложения являются существительные? придумай продолжение...
2 - 1) защитная функция белков проявляется в том, что они: 1. подвергаются...
2 - Что такое скорость определение (обозначение единицы измерения прибор)...
2 - Напишите фантастический рассказ не более 100 слов...
1 - Какой орган находится внутри позвоночника...
3 - Неизменяемые слова в словосочетании связываются с главными только...
1 - Синонимы к словам публично публиковать публичный...
1 - (а)проблема взаимодействия общества и природы приобрела в наше...
1
замена:
общее решение
частное решение