Решите данную задачу с функции Эйлера
Другие вопросы по теме Математика
Популярные вопросы
- Как написать условие одна машинистка печатает 10 страниц за...
2 - Выразить переменную a из уравнения 1\9b+1\3a=1\7...
1 - Сочинение на тему как я выполняю ) )...
1 - Прочитай і спиши позначаючи початок і кінець кожного речення?...
3 - Решите квадратное уравнение методом выделения полного квадрата....
2 - Фразеологизмы(не говорить прямо, рисковать, просить по составить...
1 - Низкопоклонство перед западом что это?...
2 - Споля урожайностью 25 ц/га собрали ячменя на 660 ц больше, чем...
1 - Вычисли периметр квадрата с длиной стороны 6 дм в 5 см...
2 - Сколько получится муки из 15,2 тонн пшеницы , если масса муки...
3
799
Пошаговое объяснение:
Приведем сначала необходимую теорию. Функция Эйлера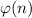 вычисляет количество натуральных чисел, меньших натурального числа n и взаимно простых с n. Ясно, что если n - простое число, то
вычисляет количество натуральных чисел, меньших натурального числа n и взаимно простых с n. Ясно, что если n - простое число, то
И, наконец,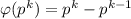 при простом p и натуральном k.
при простом p и натуральном k.
Дальше всё просто. Сосчитаем функцию Эйлера при n=2020, разложив 2020 на простые множители:
Итак, мы имеем ровно 800 натуральных чисел, меньших 2020, взаимно простых с 2020. А нас спрашивают, сколько натуральных чисел от 1 до 2018 взаимно просты с 2020. Поскольку два соседних натуральных числа не имеют общих множителей (кроме 1), 2019 взаимно просто с 2020. Поэтому ответом в задаче служит число 800-1=799.