1. Математика
  2. Решите через дискриминат

Решите через дискриминат х²+8х+15=0 у²+15у+36=0

Lungeluna Lungeluna    2   30.06.2020 08:08    5

Ответы
ivan497 ivan497  15.10.2020 15:05

Пошаговое объяснение:

х² + 8х + 15 = 0

D=b^{2} -4ac\\D=8^{2}-4*15=64-60=4\\x_{1} =\frac{-8+\sqrt{4} }{2} =\frac{-8+2}{2} =\frac{-6}{2} =-3\\x_{2} =\frac{-8-\sqrt{4} }{2} =\frac{-8-2}{2} =\frac{-10}{2} =-5

ответ: х₁ = -3; х₂ = -5.

у² + 15 у + 36 = 0

D=15^{2}-4*36=225-144=81\\y_{1} =\frac{-15+\sqrt{81} }{2} =\frac{-15+9}{2} =\frac{-6}{2} =-3\\y_{2} =\frac{-15-\sqrt{81} }{2} =\frac{-15-9}{2} =\frac{-24}{2} =-12

ответ: y₁ = -3; y₂ = -12.

ПОКАЗАТЬ ОТВЕТЫ
Zombie1466 Zombie1466  15.10.2020 15:05

Пошаговое объяснение:

x² + 8x + 15 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = 8² - 4·1·15 = 64 - 60 = 4

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁=  

x₂ =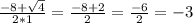 \frac{-8+\sqrt{4} }{2*1} =\frac{-8+2}{2} =\frac{-6}{2} =-3

ответ: х₁= -5; х₂= -3

y² + 15y + 36 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = 15² - 4·1·36 = 225 - 144 = 81

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

y₁ =  

y₂ =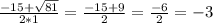   \frac{-15+\sqrt{81} }{2*1}=\frac{-15+9}{2} =\frac{-6}{2}=-3

ответ: y₁= -12; y₂= -3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Den1ska4 Den1ska4  22.04.2020 17:18
Біквадратним рівнянням є: x2+17x+7=0 17x−5 7x+5=0 7x4+17x2+5=0​...
mstasya04 mstasya04  22.04.2020 17:18
Сколько вершин,боковых граней,боковый рёбер , оснований...
milka2636 milka2636  22.04.2020 17:18
Егор ехал до школы 5 км, через 5\6 пути он догнал одноклассника, и дальше они ехали вместе, сколько км Егор ехал один?...
Dasha142nikolaeva Dasha142nikolaeva  22.04.2020 17:18
Тура пропорцияналдық кестемен берілген...
Кирвалидзе Кирвалидзе  22.04.2020 17:18
19,6 +(3-x) = 12,6X+1,5=2,818,1-x=4,612,7-(X+3)=9x-7,6=8,5​...
bIshkin bIshkin  22.04.2020 17:18
Найди число, если 8/11 его равны 2 2/11 3 30 24 6...
умняша80 умняша80  22.04.2020 17:18
AMMAIRAIMILAITTposnuu NuisnutsettesLAMA JILLEen ePashuonebungand memarer nothing intet LINE Interested.plete the seniorers ming one of the de-ords in the 20%.17confusing...
22391 22391  22.04.2020 17:18
Всем добрый день Заменить целые числа десятичными дробями 56 р. 70 к = 1760 к = 35 кг 800 г = 7 ц 54 кг = 3016 м = 6 т 80 кг = 150 800 м = 45 км 200 м = 6 т 6 ц = 9060...
NikkiLee NikkiLee  22.04.2020 17:18
За 8 часов двигаясь против течения реки катер проплыл 131, 2 км. скорость течения реки равна 1,8 км/ч. какое расстояние проплывает катер по течению реки за 3,6 часов?​...
Василий7595634 Василий7595634  22.04.2020 17:18
Запиши данное выражение без скобок (+34)+(-89)+(+93)​...

Популярные вопросы