1. Математика
  2. Решите через дискриминат

Решите через дискриминат х²-3х-10=0

embazuka embazuka    2   27.06.2020 12:59    0

Ответы
Lizard1999 Lizard1999  24.08.2020 23:46
Решение:

\boxed{{x}^{2}-3x-10=0}

Найдём дискриминант данного квадратного уравнения.

D={b}^{2}-4ac=\underbrace{{(-3)}^{2}}_{(-3)\cdot(-3)}-4\cdot1\cdot(-10)=9-(-40)=9+40=\underline{49}

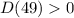Т.к. D(49)0, то наше квадратное уравнение имеет 2 корня.

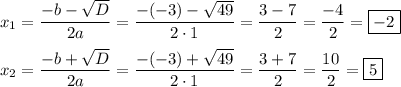
{x}_{1}=\dfrac{-b-\sqrt{D}}{2a}=\dfrac{-(-3)-\sqrt{49}}{2\cdot1}=\dfrac{3-7}{2}=\dfrac{-4}{2}=\boxed{-2} \\ \\ {x}_{2}=\dfrac{-b+\sqrt{D}}{2a}=\dfrac{-(-3)+\sqrt{49}}{2\cdot1}=\dfrac{3+7}{2}=\dfrac{10}{2}=\boxed{5}

ответ: \Large{\boxed{{x}_{1}=-2; \: \: {x}_{2}=5}}
ПОКАЗАТЬ ОТВЕТЫ
aminarowa2014 aminarowa2014  24.08.2020 23:46

Пошаговое объяснение:

x² - 3x - 10 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = (-3)² - 4·1·(-10) = 9 + 40 = 49

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁ =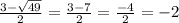 \frac{3-\sqrt{49} }{2} =\frac{3-7}{2}=\frac{-4}{2} =-2\\

x₂ =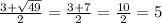\frac{3+\sqrt{49} }{2}=\frac{3+7}{2}=\frac{10}{2} =5  

ответ: х₁= -2; х₂=5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
danil200804 danil200804  13.12.2020 11:47
Найдите n если a=2^m * 3^n у которого число простых делителей m, а число натуральных делителей равно ОТВЕТЬТЕ...
Илья11345 Илья11345  13.12.2020 11:47
При делении многочлена на двучлен х - 2 остаток равен 3, при делении на 2х + 5 остаток равен 6. Найдите остаток от деления этого многочлена на (х - 2)(2х + 5)...
zlpa zlpa  13.12.2020 11:48
Заключить в скобки все слагаемые, начиная с числа х(или - х) поставив вперёд знак + 2a-b+x+c ​...
Тотах Тотах  13.12.2020 11:48
Решите задачу: 1) Три рассказа занимают 34 страницы. Первый занимает в страниц, авторой — в 3 раза меньше, чем третий. Сколько страниц занимает второйрассказ?2) Три...
d1m4Y d1m4Y  13.12.2020 11:48
Какова длина отрезка если четвере 4/5 отрезка равна 40 см​...
litoshikmari litoshikmari  13.12.2020 11:48
Расстояние между точками A и B - 390 км. Две машины одновременно выезжают из точки A и движутся в точку B. Скорость первой машины 80 км / ч, а второй - 50 км / ч....
Ilyas30rus Ilyas30rus  13.12.2020 11:49
Нужно решить тест по математике...
eldaryuldashev eldaryuldashev  13.12.2020 11:49
Преобразуйте обыкновенную дробь 281/90 в бесконечную периодическую десятичную дробь ​...
unknown2015 unknown2015  13.12.2020 11:50
на отрезке BD выбрана точка C и построены с одной стороны BD два равностороних треугольника BAC и CDE отрезки AD и CE пересекаються в точке L отрезки BE и AC в точке...
vanyabond2611 vanyabond2611  13.12.2020 11:50
Решите уравнение : х*16=384,371:х=7,22х-14х=122...

Популярные вопросы